中学2年数学 図形の調べ方 図形と証明 確認問題3・解答
3、図
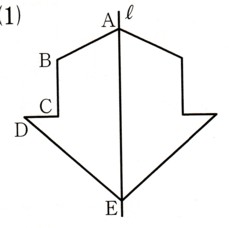
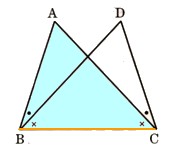
 で、∠ABD=∠DCA、∠DBC=∠ACBである。このときAC=BDであることを証明してください。
で、∠ABD=∠DCA、∠DBC=∠ACBである。このときAC=BDであることを証明してください。

 で、∠ABD=∠DCA、∠DBC=∠ACBである。このときAC=BDであることを証明してください。
で、∠ABD=∠DCA、∠DBC=∠ACBである。このときAC=BDであることを証明してください。 答え
[証明]
△ABCと△DBCにおいて
仮定より
∠DBC=∠ACB・・・①
∠DCA+∠ACB=∠ABD+∠DBC・・・②
BCは共通・・・③
①、②、③より
1辺とその両端の角がそれぞれ等しくなる。
ゆえに、
△ABC≡△DCB
よって、
合同な三角形の対応する辺の長さは等しくなりますから、
AC=BD
になります。











コメント