中学2年数学 図形の調べ方 まとめテスト5・解答
5、次の問いに答えてください。
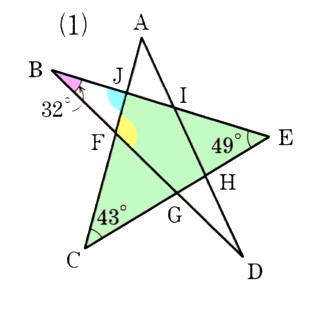
(1)図 において、∠ACE=43°、∠CEB=49°、∠EBD=32°であるとき、∠AFDの大きさを求めてください。
において、∠ACE=43°、∠CEB=49°、∠EBD=32°であるとき、∠AFDの大きさを求めてください。
 において、∠ACE=43°、∠CEB=49°、∠EBD=32°であるとき、∠AFDの大きさを求めてください。
において、∠ACE=43°、∠CEB=49°、∠EBD=32°であるとき、∠AFDの大きさを求めてください。 ∠AFDを求めるためには、
△BFJの外角になります。
∠Bと∠BJFの外角に∠AFDがなります。
∠Bは、32°とわかっていますから、
∠BJFを考えます。
∠BJFは、△JCEの外角になりますから、
∠C+∠E=∠BJF
43°+49°=92°
になります。
△BFJで考えます。
∠B+∠BJF=∠AFD
32°+ 92°=124°
答え ∠AFD=124°
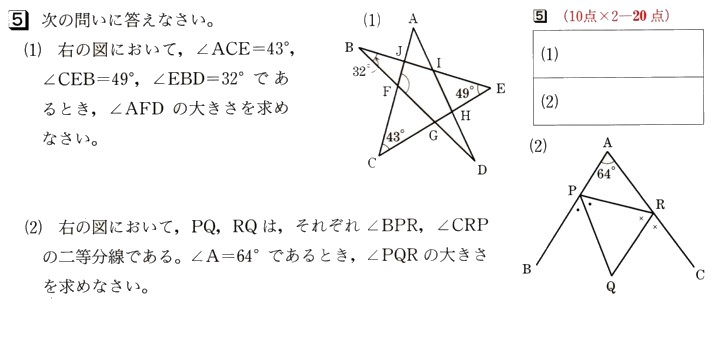
(2)図 において、PQ、RQは、それぞれ∠BPR、∠CRPの二等分線になります。∠A=64°であるとき、∠PQRの大きさを求めてください。
において、PQ、RQは、それぞれ∠BPR、∠CRPの二等分線になります。∠A=64°であるとき、∠PQRの大きさを求めてください。
 において、PQ、RQは、それぞれ∠BPR、∠CRPの二等分線になります。∠A=64°であるとき、∠PQRの大きさを求めてください。
において、PQ、RQは、それぞれ∠BPR、∠CRPの二等分線になります。∠A=64°であるとき、∠PQRの大きさを求めてください。図の●をaとし、×をbとします。
△APRについて考えます。
三角形の内角の和が180°ですから、
180°=∠A+∠P+∠R
となります、
∠A=64°
∠P=直線AB(180°)ー2a
∠R=直線AC(180°)ー2b
180°=64°+(180−2a)+(180−2b)・・・①
180=64+180−2a+180−2b
2a+2b=64+180−180+180
=244
a+b=244÷2
=122°
これで、∠RPQ+∠PRQ=a+b=122°
とわかりました。
△PQRの2つの内角の和がわかりましたから、
三角形の内角の和は180°ですから、
180°ー122°=58°
∠PQR=58°
になります。
答え ∠PQR=58°












コメント