中学２年数学 平面図形 三角形の性質 確認問題３・解答
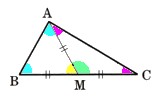
３、図
のＡＢＣにおいて、MＡ＝MＢ＝MＣであるとき、次の問いに答えてください。
のＡＢＣにおいて、MＡ＝MＢ＝MＣであるとき、次の問いに答えてください。（１）∠Ｂ＝50°のとき、∠Ｃの大きさを求めてください。
△ABMにおいて
MA=MB
ですから、
△ABM は、二等辺三角形になります。
二等辺三角形の底角はそれぞれ等しくなりますから、
∠B＝50°＝∠MAB
頂角が、∠AMBになり
180°―(50°＋50°)＝180°―100°
＝80°
次に、△MACについて考えます。
仮定により
MA=MC ですから
△MACは二等辺三角形になります。
二等辺三角形の2つの底角はそれぞれ等しくなりますから
∠C＝∠MAC
頂角は、直線BCから∠AMBを引けば∠AMCの角度がわかります。
180°―80°＝100°
＊頂角AMCは、△MABの底角の和の外角になります。
∠AMC＝∠MAB＋∠MBA
＝50°＋50°
＝100°
△MACの二等辺三角形の頂角を引けば2つの等しい底角の和になります。
180°―100°＝80°
二等辺三角形の底角はそれぞれ等しくなりますから、
80°÷2＝40°
∠MAC＝40°
∠C＝40°
答え ∠C＝40°
（２）∠Ｃ＝χ°のとき、∠MＡＢの大きさをχを用いて表してください。
図を見て（１）より
（１）より ∠Ｃ＝χ°と考えると、
△MＡＣと△MＡＢは二等辺三角形になります。
△MＡＣの外角が∠AMＢになり、
△MＡＢの外角が∠AMＣになります。
∠ＡMＢ＋∠AMＣ＝180°
∠AMＢ＝２χ°になりますから
∠AMＣ＝180°ー２χ°
二等辺三角形ですから、頂角を∠AMＢ、底角∠MＡＢ、∠MＢＡですから、
∠AMＣの１/２が∠MＡＢの角になります。
∠MＡＢ＝（180°−２χ）×1／２
＝90°ーχ°
答え 90°ーχ°
コメント