中学２年数学 円周角の定理 平面図形 確認問題７・解答
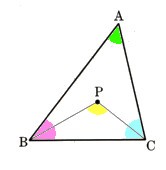
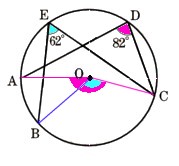
７、図
において、点Ａ,Ｂ,Ｃ,Ｄ,Ｅは半径6ｃｍの円の円周上の点になります。このときＡ⌒Ｂの長さを求めてください。ただし、Ａ⌒Ｂは短いほうの弧を示すものとします。
において、点Ａ,Ｂ,Ｃ,Ｄ,Ｅは半径6ｃｍの円の円周上の点になります。このときＡ⌒Ｂの長さを求めてください。ただし、Ａ⌒Ｂは短いほうの弧を示すものとします。 今回は、中心Ｏと点Ａ，点Ｂ、点Ｃをつなぐ補助線を引きます。
＊ 弧ＡＢの長さを求めるために、弧ＡＢの中心角を求め、半径6ｃｍの円の円周の比から弧ＡＢの長さを求めます。
まずは、弧ＡＣを考えます。
弧ＡＣの円周角は∠ＡＤＣになりますから、
∠ＡＤＣ＝82°
弧ＡＣの中心角は∠ＡＯＣになります。
中心角は円周角の2倍になりますから
∠ＡＯＣ＝∠ＡＤＣ×２
＝82°×2
＝164°
∠ＡＯＣ＝164°・・・①
つぎに、弧ＢＣの中心角を考えます。
弧ＢＣの中心角を考えます。 弧ＢＣの円周角は、∠ＢＥＣになりますから、
∠ＢＥＣ＝62°
弧ＢＣの中心角は∠ＢＯＣになります。
中心角は円周角の2倍になりますから
∠ＢＯＣ＝∠ＢＥＣ×２
＝62°×2
＝124°
∠ＢＯＣ＝124°
∠ＡＯＣから∠ＢＯＣを引けば∠ＡＯＢの角度がわかります。 164°ー124°＝40°
∠ＡＯＣ＝40°
∠ＡＯＣは弧ＡＢの中心角になります。
円周の長さは、半径6cmですから、円周は、
（半径6cmの円周）＝2×半径×π
＝2×6×π
＝12π㎝
半径6cmの円の360分の40がこの弧ABの長さにな
りますから
りますから
半径6cmの円周の長さの9分の1が弧ABの長さになります。
12π×1/9＝4/3π(㎝)
になります。
答え 4/3π(㎝)
コメント