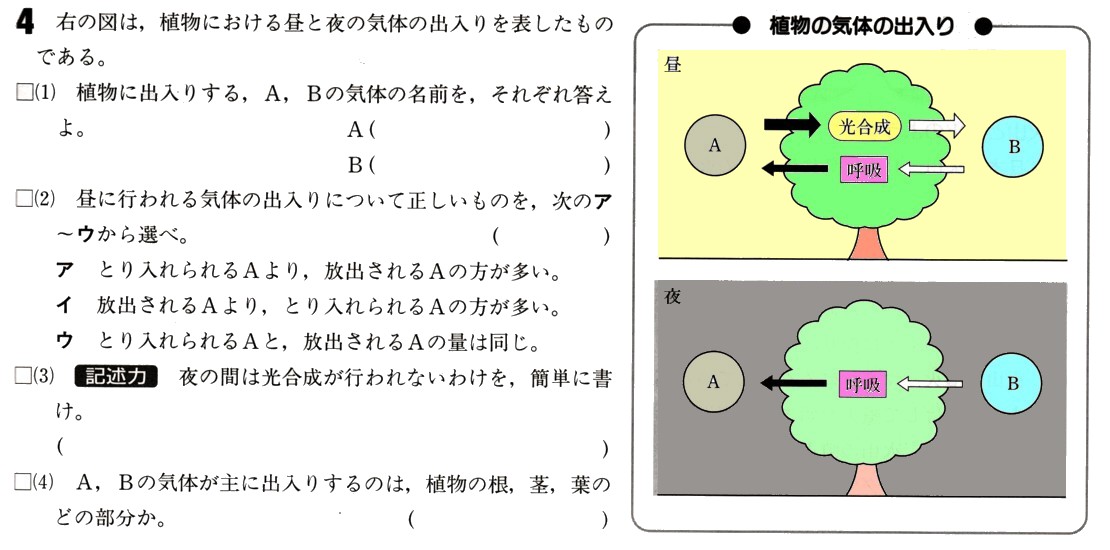
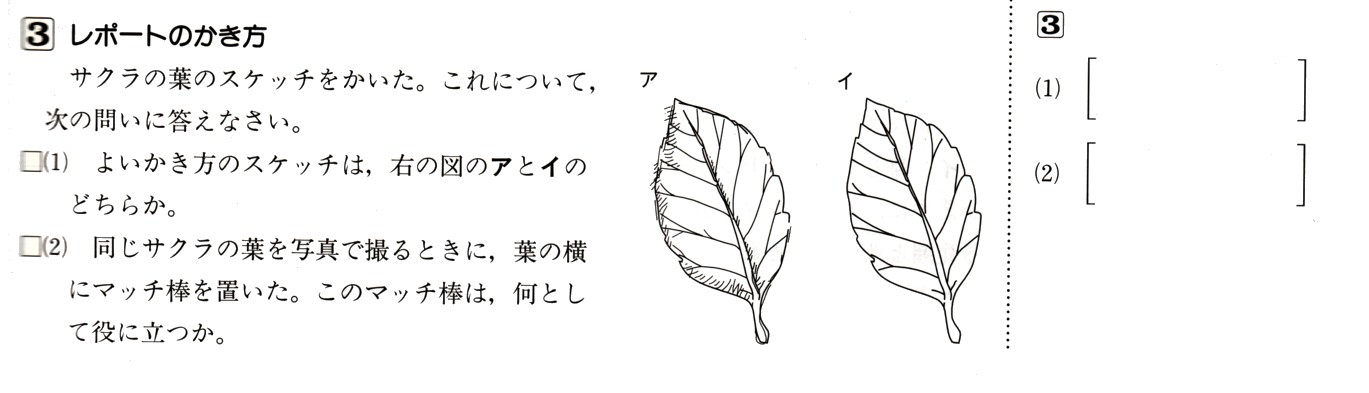
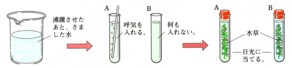
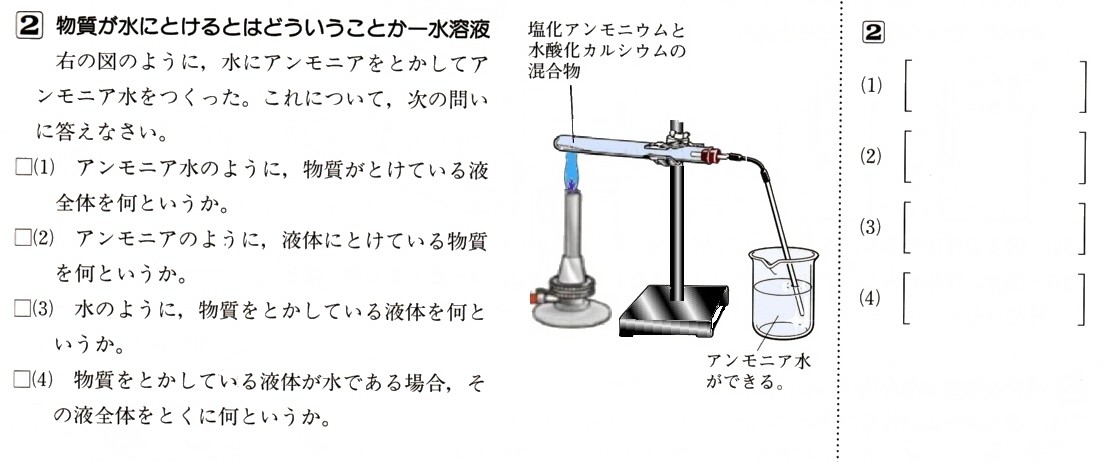
中学2年数学1(数と式,関数)のまとめ7・解答つづき
7、次の問いに答えてください。
(3)2点(4,3)(2、−1)を通る直線の式を求めてください。
直線の式は、y=aχ+b
(χ、y)=(4,3)
(χ、y) =(2、−1)
をy=aχ+bに代入します。
3=4a+b
{
−1=2a+b
4a+b=3
{
2a+b=−1
b=−4a+3
{
2a+b=−1
2a+b=−1にb=−4a+3を代入します。
2a+(−4a+3)=−1
2a−4a+3=−1
−2a=−1−3
−2a=−4
a=4/2
a=2
b=−4a+3にa=2を代入します。
b=−4×2+3
=−8+3
=−5
y=aχ+bの式に(a=2)、(b=−5)を代入します。
y=2χ−5
答え y=2χ−5
(4)2直線y=χ−6とy=−2χ+3の交点の座標を求めてください。
交点を求める場合は連立式にします。
y=χ−6
{
y=−2χ+3
χ−6=−2χ+3
χ+2χ=3+6
3χ=9
χ=9/3
χ=3
y=χ−6にχ=3を代入します。
y=3−6
y=−3
(χ、y)=(3、−3)
答え (3、−3)












コメント