中学2年数学 平面図形 2まとめテスト5・解答
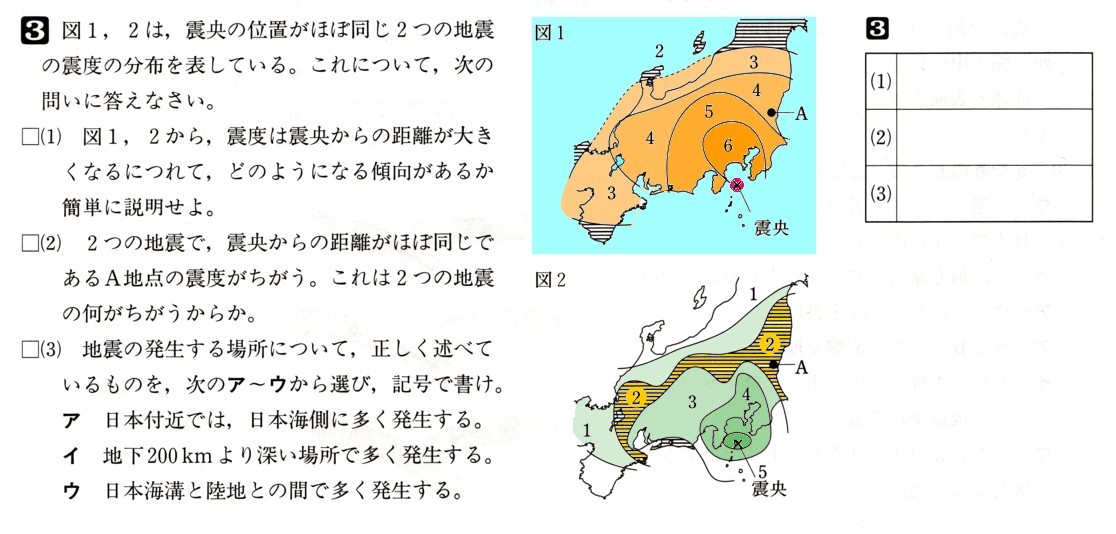
5、次の問いに答えてください。
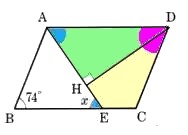
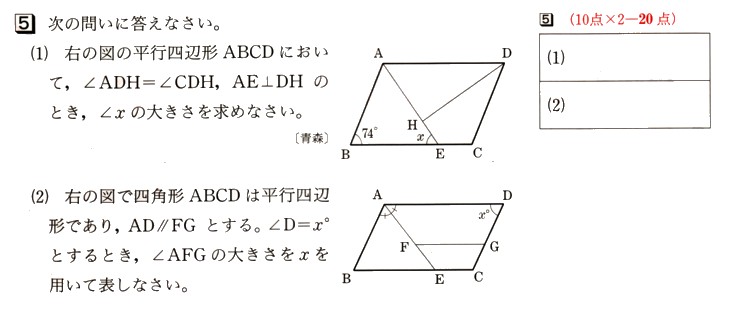
(1)図 の平行四辺形ABCDにおいて、∠ADH=∠CDH、AE⊥DHのとき、∠χの大きさを求めてください。
の平行四辺形ABCDにおいて、∠ADH=∠CDH、AE⊥DHのとき、∠χの大きさを求めてください。
ABCDは平行四辺形になりますから、
対角はそれぞれ等しくなります。それにより、∠ABC=∠ADC
∠ABC=74°ですから
∠ADC=74°になります。
∠ADHと∠CDHは二等分線で等しくなりますから
∠ADH=∠CDH
よって、∠ADH+∠CDH=74°
74°÷2=37°になり、∠ADH=37°、∠CDH=37°
になりました。
次に、∠AEBはABCDは平行四辺形ですから向かい合う2つの辺は平行ですから、
AD//BC になり
∠DAEと∠AEBは錯角により等しくなります。
∠DAE=∠AEB
△AHDについて、
三角形の内角の和は180°ですから
∠DAH=180°ー(∠ADH+∠AHD)
=180°ー(37°+90°)
=180°ー127°
=53°
∠DAE=53°ですから
∠AEB=53°
∠AEB=χですから
χ=53°になります。
答え χ=53°
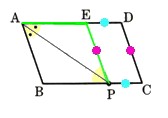
(2)図 で、四角形ABCDは平行四辺形であり、AD//FGとするとき、∠D=χ°とするとき、∠AFGの大きさをχを用いて表してください。
で、四角形ABCDは平行四辺形であり、AD//FGとするとき、∠D=χ°とするとき、∠AFGの大きさをχを用いて表してください。
まずは、平行四辺形の内角の和は360°ですから、
ABCD=360°
∠D=χ°ですから
∠B=∠D=χ°
∠A=180−χ°になります。
∠A=∠C=180°−χ°
四角形ABCD=2χ°+2(180°−χ°)
になります。
そして、四角形FGECで考えます。
∠GCE=180°−χ°(∠BADの対角)・・・?
∠CGFは、仮定より、AD//FGですから、同位角により∠ADG=∠FGC
よって、
< /p>
∠CGF=χ°・・・?
 ∠GFEは、AD//FGですから、同位角により∠DAE=∠GFE
∠GFEは、AD//FGですから、同位角により∠DAE=∠GFE
∠DAEは、∠DABの2等分線になりますから
∠DAE=∠DAB×1/2
∠DAB=180°−χ°になりますから
∠DAE=(180°−χ°)×1/2
=90°−χ°/2・・・?
∠AFG=180°ー∠GFE
=180°−(90°−χ°/2)
=180°−90°+χ°/2
=90°+χ°/2
になります。
答え ∠AFG=90°+χ°/2








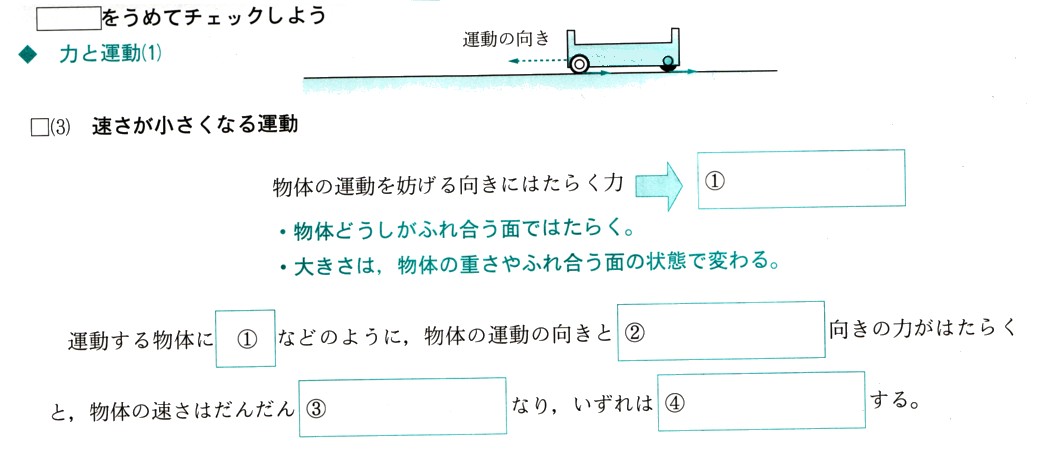


コメント