中学３年数学 関数ｙ＝ａχ² ２まとめテスト３・解答
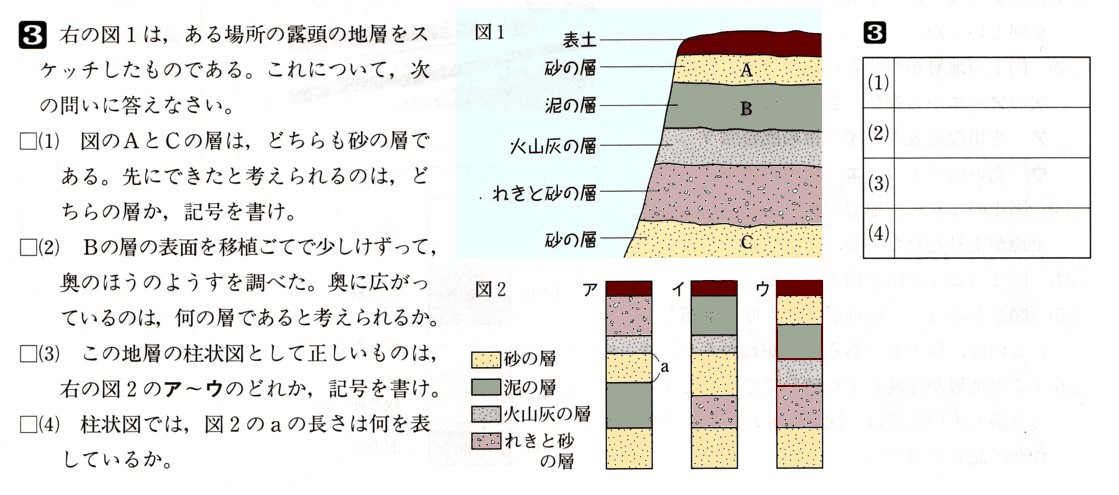
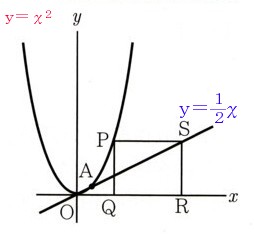
３、図
のように、放物線ｙ＝χ²と直線ｙ＝１/２χは原点と点Ａで交わっています。
点Ａから放物線上をχ座標が大きくなる方向に動く点をＰとします。
さらに、点Ｐを通りχ軸に平行な直線と直線ｙ＝１/２χとの交点をＳとします。
点Ｐ，Ｓからχ軸に垂線ＰＱ、ＳＲをそれぞれ引きます。このとき、次の問いに答えてください。
（１）Ｐのχ座標が２のとき、原点を通り、四角形ＰＱＲＳの面積を２等分する直線の式を求めてください。
まずは点Ｐ，Ｑ，Ｒ，Ｓの座標を求めます。
点Ｐのχ座標が２ですから、
ｙ＝χ²にχ＝２を代入し点Ｐのｙ座標を求めます。
ｙ＝２²
ｙ＝４
これで、点Ｐの座標（２、４）がわかり、点Ｑの座標は（２，０）となります。
点Ｓのｙ座標は点Ｐのｙ座標と同じですからｙ＝１/２χにｙ＝４を代入します。
４＝１/２χ
８＝χ
これで、点Ｓの座標（８，４）、点Ｒの座標（８，０）がわかりました。
Ｐ（２、４）
Ｑ（２，０）
Ｒ（８，０）
Ｓ（８，４）
次に考えるのは、四角形ＰＱＲＳの面積を２等分する直線とは、２つの対角線の交点になります。
χ座標は
８−２＝６
６÷２＝３
２＋３＝５
ｙ座標は
４÷２＝２
２つの対角線の交点の座標は（５，２）とわかります。
直線の式は右上がりで原点を通りますから
ｙ＝ａχ
この式に交点の座標χ＝５、ｙ＝２を代入します。
２＝５ａ
ａ＝２/５
ａは傾きですから
ｙ＝２/５χ
になります。
答え ｙ＝２/５χ
（２）点Ｐの位置により四角形ＰＱＲＳは、正方形になるときがあります。
このとき、点Ｐの座標を求めてください。
点Ｐのｙ座標をｐとするとｙ＝χ²に代入すると、χ座標はｐ²になります。
点Ｐ（ｐ、ｐ²）になります。
点Ｓのｙ座標は点Ｐのｙ座標と同じになりますから、
点Ｓのｙ座標はｐ²になります。
点Ｓのχ座標を求めるには、ｙ＝１/２χ にｙ＝ｐ²を代入します。
ｐ²＝１/２χ
χ＝２ｐ²
になります。
正方形になるにはＰＱとＰＳの長さが等しければいいということになります。
ＰＱ＝ＰＳ
ＰＱの長さは点Ｐのｙ座標になりますからＰＱ＝ｐ²
ＰＳの長さは点Ｓのχ座標から点Ｐのχ座標を引けばいいのですからＰＳ＝２ｐ²−ｐになります。
２つの式を連立方程式にします。
２ｐ²−ｐ＝ｐ²
２ｐ²−ｐ²−ｐ＝０
ｐ²−ｐ＝０
ｐ（ｐ−１）＝０
Ａ×Ｂ＝０ならばＡ＝０またはＢ＝０になります。
ｐ＝０ 、ｐ−１＝０
、ｐ＝１
ｐ＝０は条件に（正方形）合いませんからｐ＝１になります。
ｐ＝１ですから点Ｐのχ座標が１とわかりましたから、
ｙ＝χ²の式にχ＝１を代入します。
ｙ＝１²
ｙ＝１
点Ｐの座標は（１，１）になりました。
答え 点Ｐの座標は（χ、ｙ）＝（１，１）
コメント