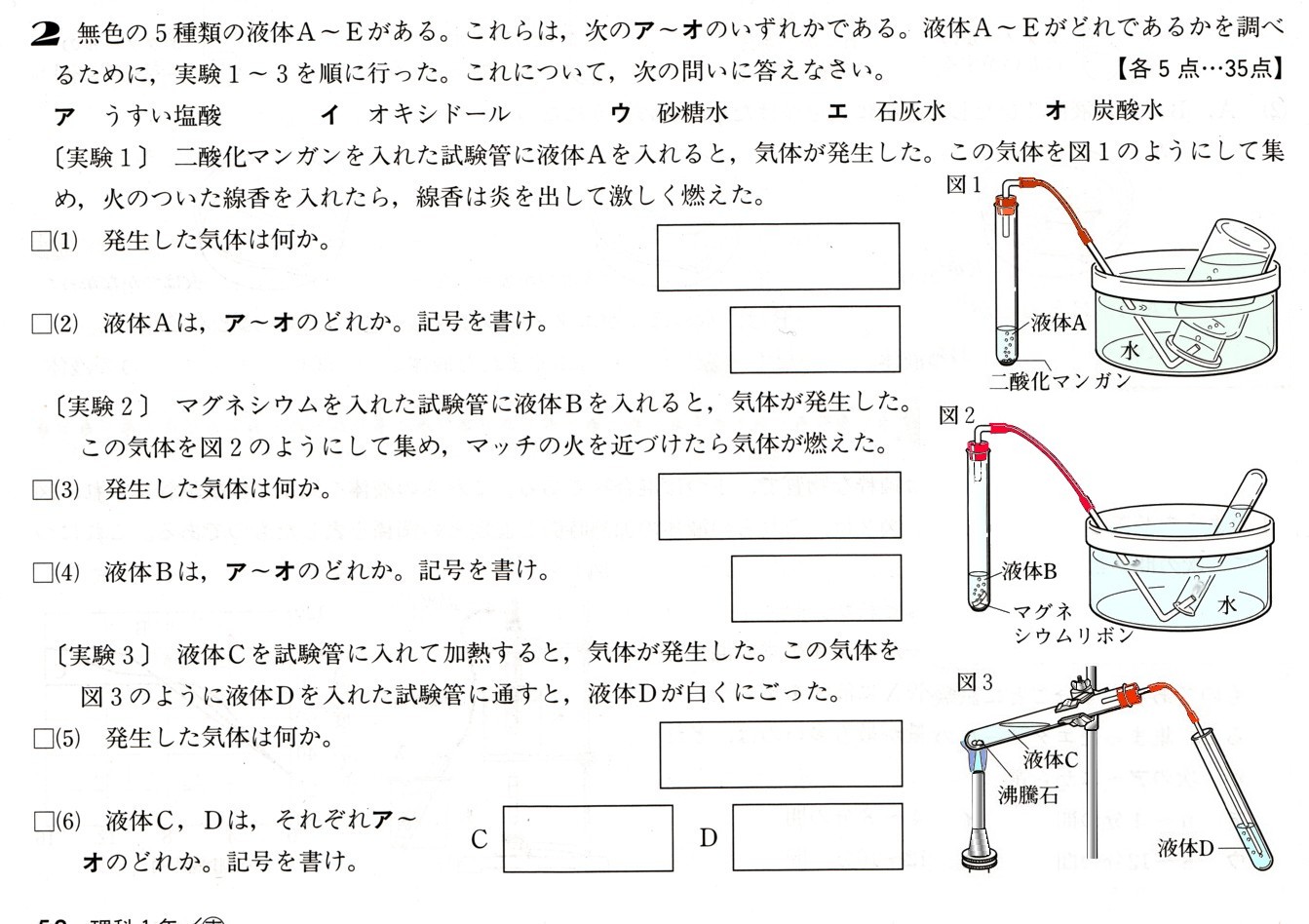
中学2年数学 図形の調べ方 2まとめテスト3・解答
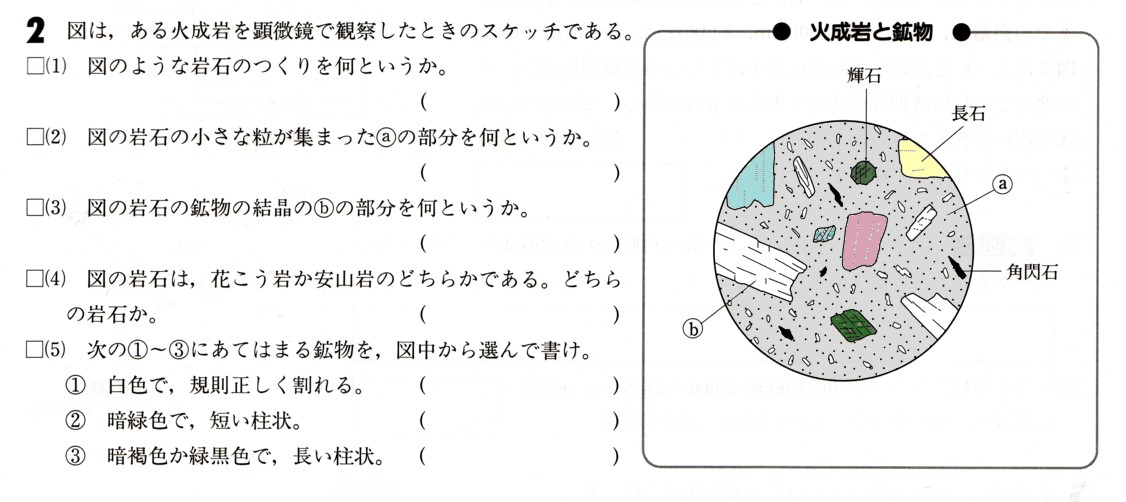
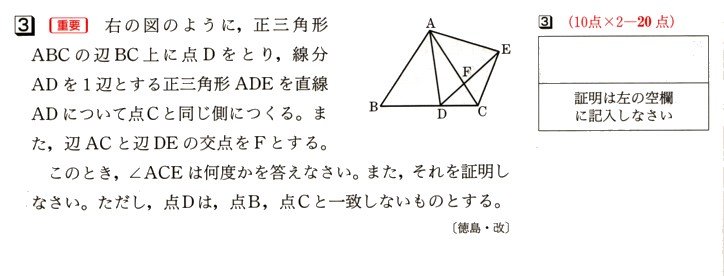
3、図 のように、正三角形ABCの辺BC上に点Dをとり、線分ADを1辺とする正三角形ADEを直線ADについて点Cと同じ側につくります。また、辺ACと辺DEの交点をFとします。
のように、正三角形ABCの辺BC上に点Dをとり、線分ADを1辺とする正三角形ADEを直線ADについて点Cと同じ側につくります。また、辺ACと辺DEの交点をFとします。
このとき、∠ACEは何度になりますか?また、それを証明してください。ただし、点Dは、点B、点Cと一致しないものとします。
 △ADBと△AECにおいて
△ADBと△AECにおいて
仮定により、
 △ABCと△ADEは正三角形ですから
△ABCと△ADEは正三角形ですから
AB=AC・・・①
AD=AE・・・②
正三角形ですから3つの角はすべて60°になります。
∠BAC=60°
∠DAE=60°
∠BAD=∠BAC−∠DAC
∠CAE=∠DAE−∠DAC
∠BAD=60°−∠DAC
∠CAE=60°−∠DAC
により、
∠BAD=∠CAE・・・③
①、②、③より
2つの辺とその間の角がそれぞれ等しくなりますから
よって、
△ADB≡△AEC
合同な三角形の対応する角はそれぞれ等しくなりますから
∠ABD=∠ACE
になります。
∠Bは、正三角形の1つの角ですから60°になりますから、
∠ACE=60°
になります。
答え ∠ACE=60°






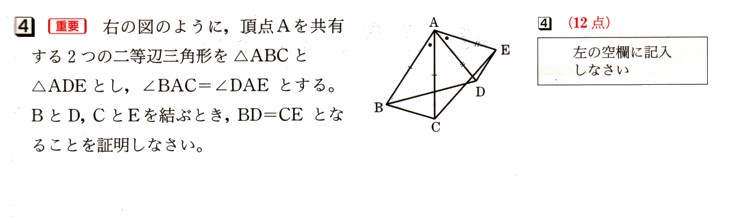
コメント