中学2年数学　1次関数　1次関数の応用　練習問題3・解答

中学2年数学　1次関数　1次関数の応用　練習問題3・解答

３、直線と図形

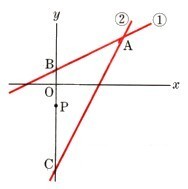
　2直線

　　χ−2ｙ＝−2　・・・?

　　ａχ−ｙ＝3　・・・?

　　が交わっています。また、直線?、?とｙ軸との交点をそれぞれＢ，Ｃとします。△ＡＢＣの面積が8であるとき、次の問いに答えて下さい。

（１）点Ａの座標とａの値を求めて下さい。

　　点Ａの座標を求めるには、2直線の交点の座標になります。

　2直線の交点は?，?の連立方程式のχ,ｙになります。

　　　χ−2ｙ＝−2
　｛
　　　ａχ−ｙ＝3

　　の式を、ｙ＝～の形にします。

　　　−2ｙ＝−χ−2

　　　　ｙ＝1/2 χ ＋1・・・?

　　　−ｙ＝−ａχ＋3

　　　　ｙ＝ａχ−3　・・・?

　ｙ＝ａχ＋ｂ

　ｙ＝(傾き)χ＋(切片)

　　?の(切片)は＋1

　　?の(切片)は−3

　　△ＡＢＣの底辺を辺ＢＣとすると、4　になります。

　　△ＡＢＣの面積が8　ですから、

　　（△ＡＢＣの面積が8）＝（底辺）　４×　（高さ）　÷　2

　　　　　　　　　　　　8＝2(高さ)

　　　(高さ)＝4

　　点Ａの座標のχの座標が4とわかりました。

　　ｙ＝1/2 χ ＋1　・・・?　の式に　χ＝4　を代入します。

　　　ｙ＝3

　　ｙ＝ａχ−3　・・・?　の式に　χ＝4　ｙ＝3　を代入します。

　　3＝4ａ−3

　　4ａ−3＝3

　　4ａ＝3＋3

　　ａ＝3/2

　　　答え　ａ＝3/2

（２）△ＡＢＯと△ＡＣＯの面積比を求めて下さい。

　　　三角形の面積比は、△ＡＢＯ：△ＡＣＯ＝ＢＯ：ＣＯ

　　になります。

　　　△ＡＢＯと△ＡＣＯ　の底辺をｙ軸と考えるとＯＢは、1　ＣＯは、3　になります。

　　高さは同じですから、面積比も、底面の比と同じになります。

　　1：3＝ＢＯ：ＣＯ＝△ＡＢＯ：△ＡＣＯ

　　　答え　△ＡＢＯ：△ＡＣＯ＝　1：3 

（３）線分ＢＣ上に点Ｐをとります。直線ＡＰが△ＡＢＣの面積を2等分するとき、直線ＡＰの式を求めて下さい。

　　
　　△ＡＢＰ＝△ＡＣＰ　面積が同じということは、ＢＣを（底辺）にしたとき、高さは同じですから、

　底辺の長さも同じになりま
す。

　　ＢＣの長さは、点Ｂ（0,1）点Ｃ（0、−3）ですから、長さは４になります、その中点は、2になりますから、

　　点Ｐは、(0、−1)になります。

　　　これで直線ＡＰの式の(切片)がわかりました。

　　次は傾きになります。傾きは、点Ａで重なりますから、点Ａの座標と、Ｐの座標を　ｙ＝ａχ＋ｂ　の式に代入して、

　　連立方程式にして傾きを見つけます。

　　座標Ａ　　　　　
　　　　　　χ−2ｙ＝−2
　　　　｛
　　　　　　3/2χ−ｙ＝3

　　　　　　χ−2ｙ＝−2
　　　　　｛
　　　　　　3χ−2ｙ＝6

　　　χ−2ｙ＝−2
　−)3χ−2ｙ＝6
　　−2χ　　＝−8

　　χ＝4

　　χ−2ｙ＝−2　に　χ＝4　を代入します。

　　(4)−2ｙ＝−2

　　−2ｙ＝−2−4

　　−2ｙ＝−6

　　　ｙ＝3

　　　座標Ａ　（４，３）とわかりました。

　　　座標Ｐ　は　(0、−1)

　　ｙ＝ａχ＋ｂ　の式に代入します。
　　

　　　　3＝4ａ＋ｂ
　　｛
　　　　ｂ＝−1

　　　3＝4ａ＋ｂ　に　ｂ＝−1　を代入します。

　　　3＝4ａ＋(−1)

　　　4ａ＋(−1)＝3

　　　4ａ＝3＋1

　　　ａ＝1

　　　　傾きもわかりました。

　　　　(傾き)　1

　　　　(切片)　−1

　　　右上がりのグラフになりますから符合は（＋）になります。

　　　ｙ＝χ−1

　　直線ＡＰの式がわかりました。

　　　答え　ｙ＝χ−1