中学２年数学 円周角の定理 平面図形 確認問題４・解答
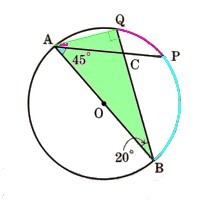
４、図
において、ABは円Оの直径であり、A⌒B上に2点P,Qを∠PAB＝45°、∠ABQ＝20°となるようにとります。このとき、B⌒Pの長さは、P⌒Qの長さの何倍になりますか？
において、ABは円Оの直径であり、A⌒B上に2点P,Qを∠PAB＝45°、∠ABQ＝20°となるようにとります。このとき、B⌒Pの長さは、P⌒Qの長さの何倍になりますか？ 弧の長さの比を考えるとき、
まずは、円周角の角度をだし、その角度の比から弧の長さの比をだします。
弧PBの円周角は45°・・・①
弧PQの円周角は、まだわかりません！
そのために、まずは点A、点Qを補助線でつなぎます。
そして、△AQCの∠Aの角度がわかれば弧QPの長さを比から導けます。
∠Qから考えます。
∠Q は弧ABの円周角になり、中心角は直線になります。
中心角は180°ですから、円周角は半分の角度になります。
∠Q＝AB×1/2
＝180°×1/2
＝90°
次に、∠QCAを考えます。
∠QCAは△CABの∠CABと∠CBAの2つの内角の和の外角になります。
∠QCA＝∠CAB＋∠CBA
＝45°＋20°
＝65°
三角形の内角の和は180°ですから
∠QAC＝180−（∠Q＋∠QCA）
＝180−(90°+65°)
＝180−155°
＝25°・・・②
弧PB＝45°・・・①
弧PQ＝25°・・・②
より、
45÷25＝1.8
弧PBは弧PQの1.8倍になることがわかりました。
答え 1.8倍
コメント