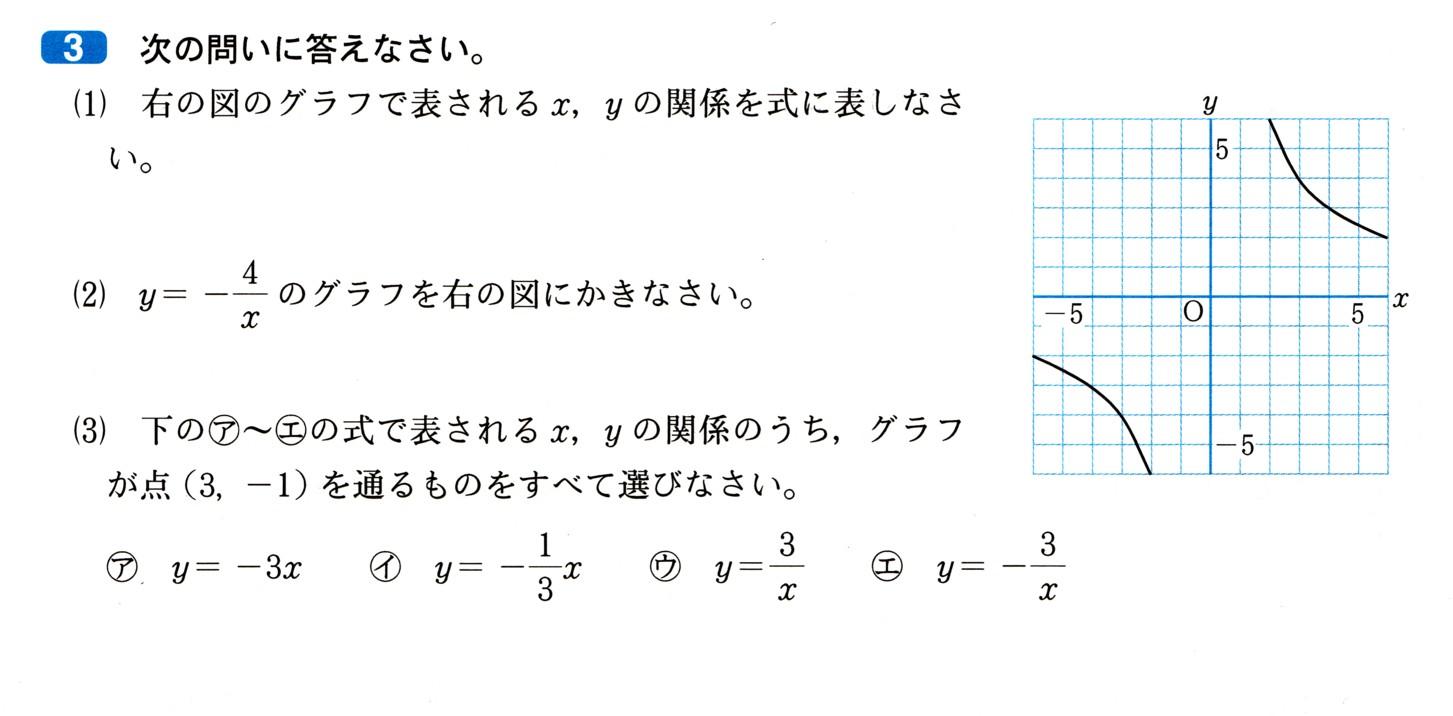
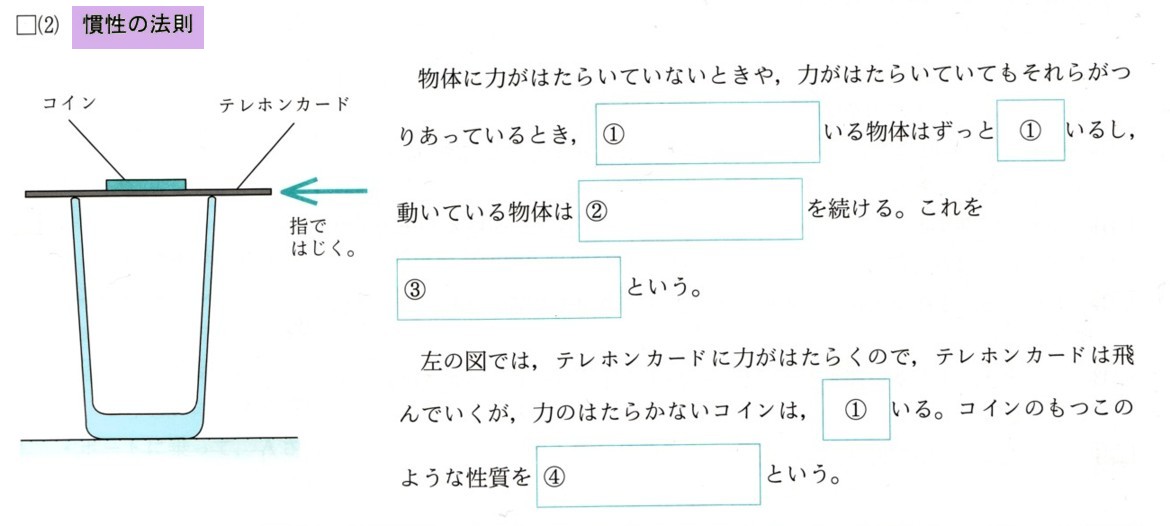
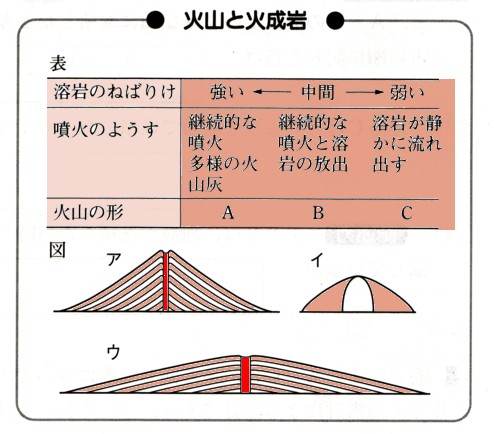
中学２年数学　平行四辺形の性質　練習問題４・解答

中学２年数学　平行四辺形の性質　練習問題４・解答

４、平行四辺形と合同

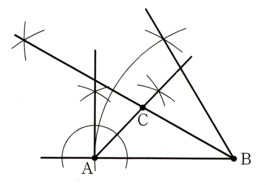
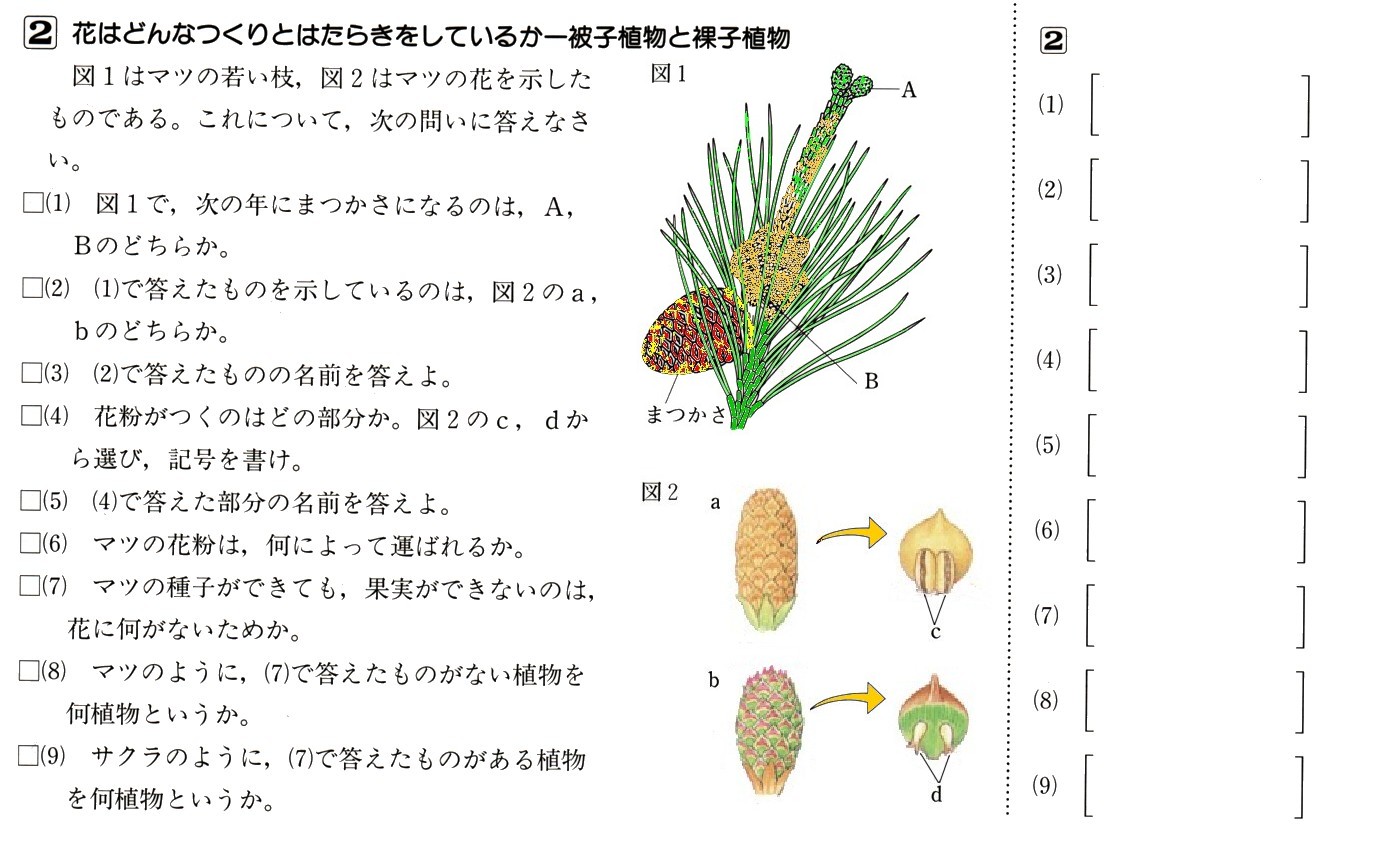
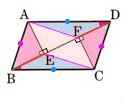
図のように、平行四辺形ＡＢＣＤの対角線ＢＤに、Ａ、Ｃからそれぞれ垂線ＡＥ、ＣＦを引くとき、四角形ＡＥＣＦは平行四辺形になることを証明してください。

答え

〔証明〕

△ＡＢＥと△ＣＤＦにおいて

仮定より

△ＡＢＥと△ＣＤＦは、

∠ＡＥＢ＝90°

∠ＣＤＦ＝90°

∠ＡＥＢ＝∠ＣＤＦ

になり、

△ＡＢＥと△ＣＤＦは直角三角形になります。

□ＡＢＣＤは平行四辺形ですから、

ＡＢ//ＣＤ

錯角により

∠ＡＢＥ＝∠ＣＤＦ・・・①

□ＡＢＣＤは平行四辺形ですから、

ＡＢ＝ＣＤ・・・②

①、②より

直角三角形は、斜辺とその他の鋭角がそれぞれ等しくなりますから

△ＡＢＥ≡△ＣＤＦ

になります。

合同な三角形の対応する辺はそれぞれ等しくなりますから

ＡＥ＝ＣＦ・・・③

つぎに、ＡＥ⊥ＢＥ、ＣＦ⊥ＤＦ・・・④

ですから、

辺ＡＥと辺ＣＦは角度も同じになります。

よって、③、④より

四角形ＡＥＣＦは向かい合う辺が平行で、長さが等しくなりますから、

四角形ＡＥＣＦは平行四辺形ということがわかります。