中学2年数学 平面図形 平行四辺形の性質 確認問題4・解答
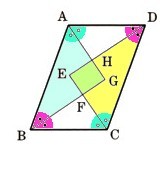
4、図 のように、平行四辺形ABCDの∠A、∠B、∠C、∠Dの二等分線によってつくられる四角形EFGHは、長方形であることを証明してください。
のように、平行四辺形ABCDの∠A、∠B、∠C、∠Dの二等分線によってつくられる四角形EFGHは、長方形であることを証明してください。
長方形であることを証明するためには4つの角が90°であれば長方形であると証明できます。
答え
〔証明〕
四角形ABCDの内角の和は360°ですから
平行四辺形は向かい合う角はそれぞれ等しくなりますから
○○+●●=∠A+∠B=180°
○+●=∠A×1/2+∠B×1/2=180°×1/2
=90°
○+●=90°・・・①
△AGBと△CEDにおいて
①より
∠GAB+∠GBA=90°
∠AGB=180°ー(∠GAB+∠GBA)
∠AGB=180°ー90°
∠AGB=90°・・・②
∠EDC+∠ECD=90°
∠DEC=180°ー(∠EDC+∠ECD)
∠DEC
=180°ー90°
∠DEC=90°・・・③
次に、△ADHと△CBFにおいて
①より
∠AHD=180°ー(∠DAH+∠ADH)
∠AHD=180°ー90°
∠AHD=90°
対頂角により
∠EHG=∠AHD
∠EHG=90°・・・④
∠BFC=180°ー(∠FBC+∠FCB)
∠BFC=180°ー90°
∠BFC=90°
対頂角により
∠EFG=∠BFC
∠EFG=90°・・・⑤
②、③、④、⑤より
4つの角が等しい四角形ですから、
EFGHは長方形ということがわかります。










コメント