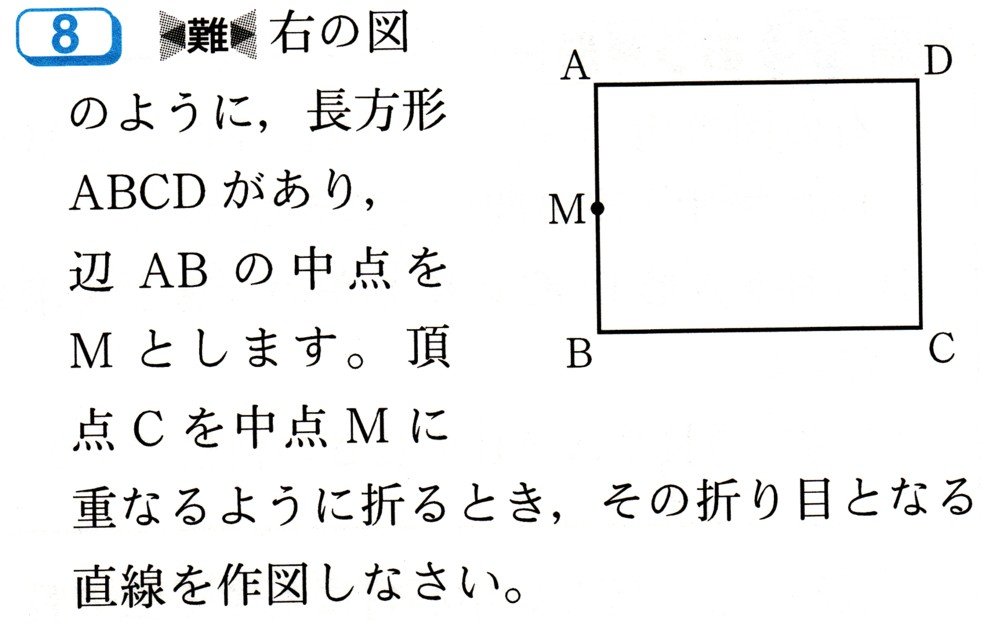
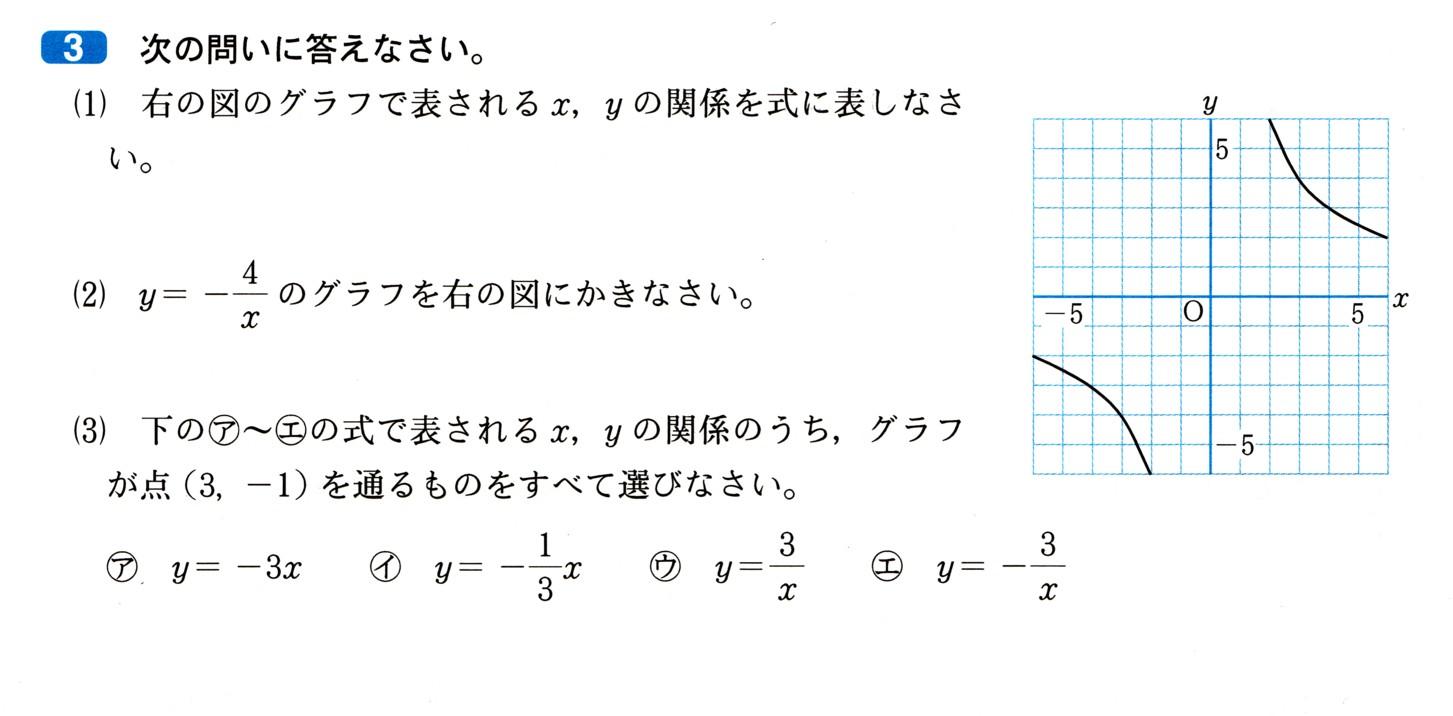
中学3年数学 変化の割合の計算、交点の座標 練習問題1・解答
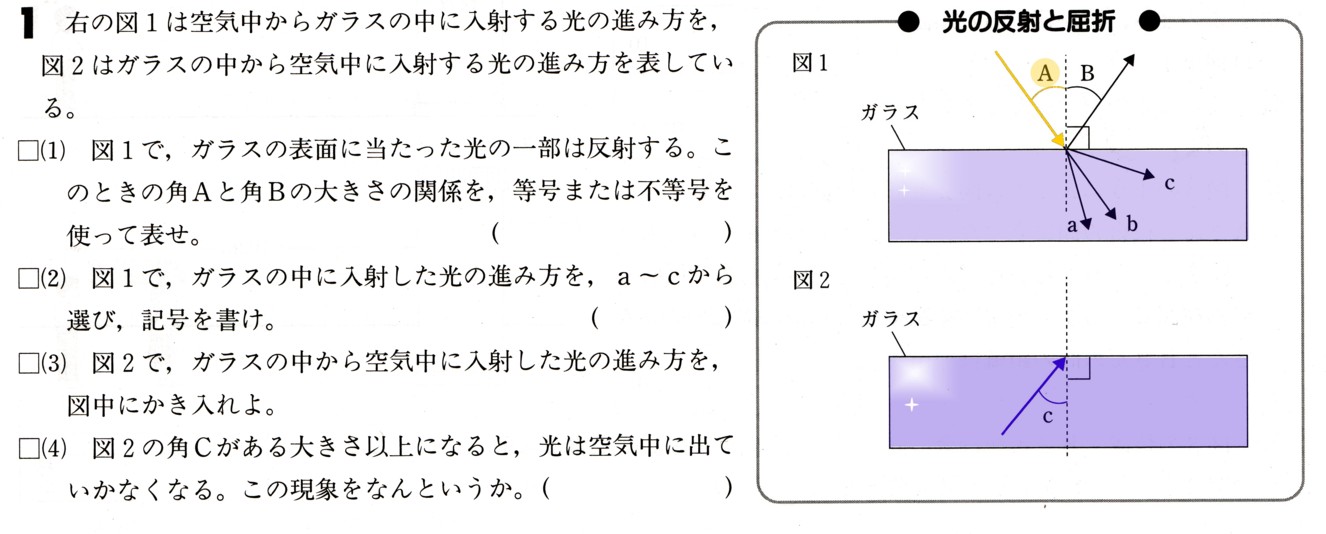
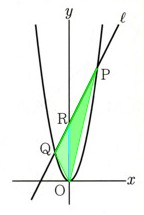
1、図 で、点P,Qは関数y=aχ²のグラフと直線ℓとの交点になります。
で、点P,Qは関数y=aχ²のグラフと直線ℓとの交点になります。
点Rは直線ℓとy軸との交点になり、y軸の正の部分で交わっています。
P(2,8)であり、△OPRと△OQRとの面積の比は2:1になります。
このとき、次の問いに答えてください。
(1)aの値を求めてください。
y=aχ²の式のPの座標(2,8)を代入します。
8=2²a
4a=8
a=8/4
a=2
答え a=2
(2)この関数について、χの値が−1から2まで増加するときの変化の割合を求めてください。
関数y=aχ²の変化の割合
χの値がpからqまで増加するとき、
変化の割合=a(p+q)
で求めることができます。
この関数 y=2χ²の係数は2とわかりましたから。このグラフの式は
y=2χ² となります。
この式を使い変化の割合を考えていきます。
2(−1+2)=(変化の割合)
2×1=2
変化の割合は2となります。
答え 2
(3) △OPQの面積を求めてください。
△OPQの面積を求めてください。
△OPRと△OQRの2つの3角形で考えます。
2つの三角形の底辺をORとして考えると、
2つの三角形の底辺は同じになり、△OPRと△OQRの面積の比は2:1
ですから、2つの三角形の高さの比が2:1となります。
△OPR高さはP座標のχの値になりますからχ=2となります。
面積の比が2:1ですから△OQRの高さがχ=−1で1となります。
次に底辺の長さを考えます。
底辺の長さは直線ℓの切片になります。
直線ℓの式はy=aχ+b
○関数y=aχ²と2点で交わる直線の傾きは、その2点間の変化の割合に等しくなります。
よって、交点のχ座標がp、qのとき、直線の傾きはa(p+q)で求めることができます。
これにより、(2)でy=aχ²の変化の割合がわかりましたから、
直線y=aχ+bの傾きがわかります。
y=2χ+b
この式に点Pの座標を代入すると切片(ORの長さ)がわかります。
8=2×2+b
8=4+b
b=8−4
b=4
ORの高さは4とわかりました。
△OPRと△OQRの面積は(OR×2÷2)+(OR×1÷2)
(4×2÷2)+(4×1÷2)=4+2=6
答え 6








コメント