中学3年数学 三平方の定理の利用 確認問題4・解答
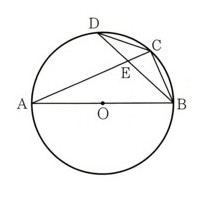
4、 図のように、線分ABと直径とする半径5の円Oの円周上に、2点C,DをBC=CD=4であるようにとります。
図のように、線分ABと直径とする半径5の円Oの円周上に、2点C,DをBC=CD=4であるようにとります。
また、線分ACと線分BDの交点をEとします。このとき、次の問いに答えてください。
(1)CE=χとすると、BEをχの一次式で表してください。
△EDCと△EBAで
弦BCで考えます。
∠BDC=∠BAC(円周角が同じ)・・・?
∠AEB=∠CED(対頂角)・・・?
?,?より
2組の角がそれぞれ等しくなりますから
△EDC∽△EBA
になります。
そうすると、AB:DC=BE:CE
AB(半径が5ですから)=10
DC=4
10:4=5:2
5:2=BE:χ
5×χ=BE×2
BE=5χ/2
答え BE=5χ/2
(2)CEの長さを求めてください。
△BECで考えます。
△BECは、弦ABで考えると円周角は90゜になり、
△BECは直角三角形ということがわかります。
直角三角形の辺の比は、1:2:√3=(底辺):(斜辺):(高さ)
底辺=CE
斜辺=BE
高さ=BC
CEをχとして考えます。
CE=χ
BE=5χ/2 (1)により
BC=4 (仮定より)
三平方の定理を利用してCEの長さを求めます。
(底辺)²+(高さ)²=(斜辺)²
(χ)²+(4)²=(5χ/2)²
χ²+16=25χ²/4
4χ₂+64=25χ²
25χ²−4χ²=64
21χ²=64
χ²=64/21
χ=√64/21(χは+になります)
χ=√64×21/√21×√21
χ=√1344/21
2)1344
2) 672
2) 336
2) 168
2) 84
2) 42
21
χ=8√21/21
答え CEの長さは、8√21/21











コメント