中学3年数学 三平方の定理の利用 3確認問題3・解答
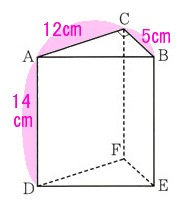
3、次の図 のような、△ABCを1つの底面とする三角柱があります。
のような、△ABCを1つの底面とする三角柱があります。
この三角柱において、∠ACB=90゜、AC=12?、BC=5?、AD=14?で、
側面はすべて長方形になります。このとき次の問いに答えてください。
(1)この立体の表面積を求めてください。
まずは、上底の面積を求めます。
(上底の面積)=5×12×1/2=30㎠
(上底と下底の面積)=30×2=60㎠・・・?
次に側面積を求めます。
ABの長さは三平方の定理を利用して求めます。
(底辺)²+(高さ)²=(斜辺)²
底辺=CB=5cm
高さ=CA=12cm
斜辺=AB=χ?
5²+12²=χ²
25+144=χ²
169=χ²
χ=13(χは+になります)
AB=13?
(横の長さ)=(AB)+(BC)+(CA)
AB=13?
BC=5cm
CA=12cm
13+5+12=30?
(縦の長さ)=AD=14?
(側面積)=30×14=420㎠・・・?
三角柱の表面積=?+?
60+420=480㎠
答え 480㎠
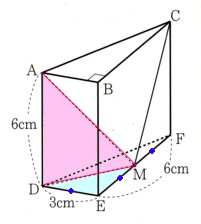
(2)点Aから辺BE,CFを通り点Dまで紐をかけます。紐の長さが最も短くなるとき、
その長さを求めてください。
次の図 のようになります。
のようになります。
横の長さは△ABCの周の長さになり
縦の長さはAD=14?
になります。
(1)より
AB=13?
BC=5cm
CA=12cm
13+5+12=30?・・・?
三平方の定理を利用し△ADDを考えます。
底辺=(横の長さ)=30?
高さ=AD=14?
斜辺=赤紐=χ?
(底辺)²+(高さ)²=(斜辺)²
30²+14²=χ²
900+196=χ²
1096=χ²
χ=√1096(χは+になります)
2
)1096
2) 548
274
χ=2√274
紐の長さが最も短くなる場合の紐の長さは、2√274?になります。
答え 2√274?














コメント