中学3年数学 三平方の定理 確認問題2・解答
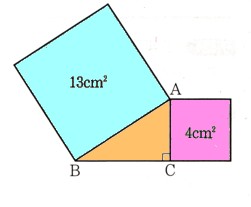
2、次の図 の△ABCは∠C=90゜の直角三角形で、2辺AB,ACを1辺とする正方形の面積は、
の△ABCは∠C=90゜の直角三角形で、2辺AB,ACを1辺とする正方形の面積は、
それぞれ13㎠、4㎠になります。このとき、次の問いに答えてください。
(1)辺BCを1辺とする正方形の面積を求めてください。
BCの長さを求めるには、△ABCの辺AB,ACの長さがわかればBCの長さがわかります。
まずは、辺ABから考えていきます。
正方形の面積は、1辺×1辺=正方形の面積=1辺²
1辺の長さをχとして考えます。
13㎠=χ²
χ=±√13?(χは+ですから)
χ=√13?
次にACの辺を考えます。
1辺の長さをχとして考えます。
4㎠=χ²
χ=±2?(χは+ですから)
これで、2つの辺、斜辺と直角を挟む2つの辺の1つがわかりました。
わからない残りの辺の長さをχとして三平方の定理を利用して考えます。
斜辺AB=√13?
辺AC=2cm
辺BC=χ?
χ²+2²=(√13)²
χ²+4=13
χ²=13−4
χ²=9
χ=±3?(χは+ですから)
χ=3cm
辺BCを1辺とする正方形の面積は、
(辺BC)²=辺BCを1辺とする正方形の面積
BC=3cm
3²=9㎠
答え 9㎠
(2)△ABCの3辺の長さを求めてください。
(1)ですべての辺の長さがわかりましたから、
答え
辺AB=√13?、辺AC=2?、辺BC=3?









コメント