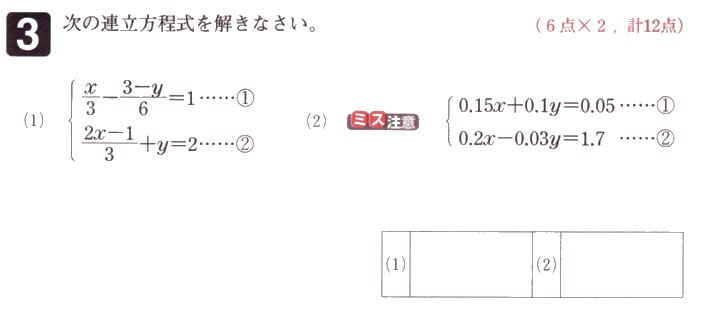
中学1年数学 立体の表面積と体積 練習問題2 解答・解説
次の文、または展開図で表された立体の表面積を求めてください。
(1)底面の半径が4cm、母線の長さが6?の円錐。
まずは、展開図で考えましょう。
表面積は、三角錐の場合、底面の円の面積と側面のおうぎ形の面積になります。
(三角錐の表面積)=(底面の面積)+(側面の面積)
?(底面の面積)=(円の面積)
?(側面の面積)=(おうぎ形の面積)
(三角錐の表面積)=(円の面積)+(おうぎ形の面積)
(円の面積)=πγ²
=(半径)×(半径)×π
=4×4×π
=16π?²
つぎに、おうぎ形の面積を考えます
おうぎ形の面積を求める式は
(おうぎ形の面積)=πγ²×中心角/360
=(半径)×(半径)×π×中心角/360
おうぎ形の半径は、母線の長さになりますから、半径は6cmということがわかります
=6×6×π×中心角/360
中心角は、底辺の円周の長さと、おうぎ形の弧の長さは等しくなっていますから
(底辺の円周)=(おうぎ形のこの長さ) になります
底辺の円周を求める式は
(円周)=2×(半径)×π
おうぎ形の弧の長さを求める式は
(弧の長さ)=2πγ×中心角/360
=2×(半径)×π×中心角/360
中心角を求めるのですから、中心角をχ゜と考えます。
(円周)=(弧の長さ)
2×(半径)×π=2×(半径)×π×中心角/360
2×(半径)×π=2×(半径)×π×χ゜/360
底辺の円の半径は4cmで、おうぎ形の半径は母線の6cmになります
2×4×π=2×6×π×χ゜/360
になります。
8π=12π×χ゜/360
両辺に360をかけます
360×8π=12π×360×χ゜/360
両辺に1/12πをかけます
1/12π×360×8π=1/12π×12π×360×χ゜/360
240=χ
これで、おうぎ形の中心角がわかりました。
それでは、側面のおうぎ形の面積を求めましょう。
おうぎ形の面積を求める式は。
m=πγ²×中心角/360 でしたね
(おうぎ形の面積)=(半径)×(半径)×π×中心角/360
おうぎ形の半径は、母線の長さになりますから、6cm
おうぎ形の中心角は、240゜ ですから
=6×6×π×240/360
=36π×2/3
=24πcm²
これで側面のおうぎ形の面積がわかりました。
円錐の表面積は
(円錐の表面積)=(底面の面積)+(側面の面積)
ですから、
(円錐の表面積)=16π?²+24πcm²
=40π?²
答え 40π?²
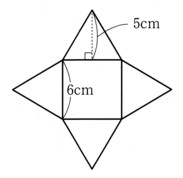
(2)正四角錐
正四角錐の表面積は
底面積+側面積 になります。
底面積は正四角錐ですから
正方形になります。
正方形の面積は、4辺の長さがそれぞれ等しくなりますから。
1辺の長さが6cmですから。
(正方形の面積)=(1辺)×(1辺)
=6cm×6cm
=36cm²
次に側面積を求めます。
側面積は、それぞれ等しい、4つの二等辺三角形になります。
(側面積)=4×(二等辺三角形の面積)
三角形の面積を求める式は
(三角形の面積)=(底辺)×(高さ)×1/2
底辺は6cm 、高さは5cmですから
=6×5×1/2
=15?²
これで、1つの面の三角形の面積がわかりましたから
(側面積)=4×(二等辺三角形の面積)
=4×15?²
=60?²
側面の面積もわかりました。
正四角錐の表面積は
(正四角錐の表面積)=(底面積)+(側面積)
=36?²+60?²
=96?²
答え 96?²
(3)円錐
円錐の表面積の求め方は
(円錐の表面積)=(底面積)+(おうぎ形の面積)
になります。
(底面積)=(円の面積)
(側面積)=(おうぎ形の面積)
今回は底面の円の半径がわかりませんから。
わかっているおうぎ形の半径6cmで考えていきましょう
おうぎ形の面積は
(おうぎ形の面積)=πγ²×中心角/360
おうぎ形の半径は、6cm
中心角は、直線になりますから180゜になります
(おうぎ形の面積)=(半径)×(半径)×π×中心角/360
=6×6×π×180/360
=36π×1/2
=18π?²
になります。
次に円の面積を考えます
円の面積は、
(円の面積)=πγ²
=(半径)×(半径)×π
半径がおうぎ形の弧の長さと、底面の円の円周の長さが等しくなります。
この円の周を求める式
(円周の長さ)=2×(半径)×π
から、底面の円の半径がわかります。
それでは、おうぎ形の弧の長さから考えます。
(おうぎ形の弧の長さ)=2πγ×中心角/360
=2×(半径)×π×中心角/360
おうぎ形の半径は6cm、おうぎ形の中心角は180゜
=2×6×π×180/360
=12π×1/2
=6πcm
これで、おうぎ形の弧の長さが6πcmとわかりました。
(おうぎ形の弧の長さ)=(円周)
ですから
(円周)=6πcm
になります。
円周を求める式は
(円周の長さ)=2×(半径)×π
ですから、
6πcm=2×(半径)×π
になります。
両辺に1/2をかけます
1/2×6πcm=1/2×2×(半径)×π
両辺に1/πをかけます
1/π×1/2×6πcm=1/2×2×(半径)×1/π×π
3cm=(半径)
これで、底面の円の半径がわかりました
円の面積を求める式は
(円の面積)=πγ²
=(半径)×(半径)×π
半径は、3cmとわかりましたから
=3×3×π
=9πcm²
これで、底面の円の面積が9πcm²とわかりました。
(円錐の表面積)=(底面積)+(おうぎ形の面積)
ですから、
(円錐の表面積)=9πcm²+18π?²
=27πcm²
答え 27πcm²










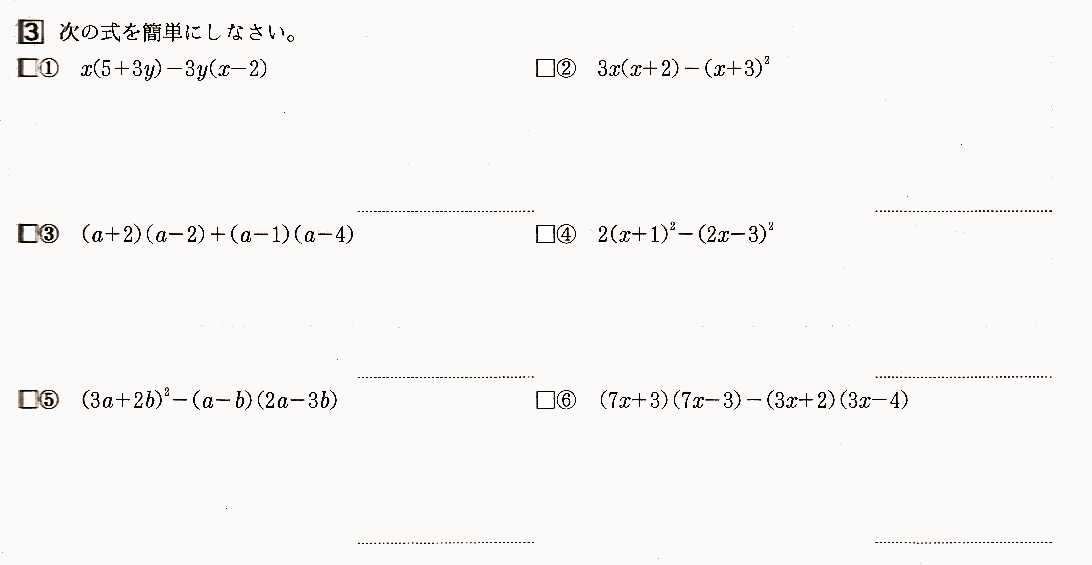


コメント