中学1年数学 立体の表面積と体積 確認問題3 解答・解説
次の問いに答えてください
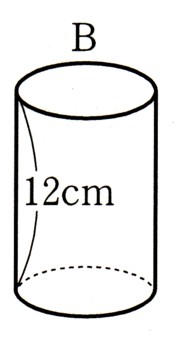
(1)底面の半径が5cmで、体積が100πcm³の円柱の表面積を求めてください。
この問題をといていく流れから考えていきます。
まずはたずねているのは、円柱の表面積です。
ですが、この円柱の表面積を求めるために、わかっていることは、底面の円の半径のみです。
ただし、体積がわかっていますから、体積から底面の面積、円周の長さ、側面の辺の
長さなどを求めていきたいと思います。
まずは、体積から考えていきます。
体積を求める式を利用します
円柱の体積を求める式は
(体積)=Sh
=(底面積)×(高さ)
底面積は、円ですから円の面積は
(円の面積)=πγ²
=(半径)×(半径)×π
=5×5×π
=25πcm²
体積が、100πcm³ですから、
(100πcm³)=25πcm²×(高さ)
になります。
両辺に1/25πをかけます
1/25π×100πcm³=1/25π×25πcm²×(高さ)
4cm=(高さ)
これで、この円柱の高さがわかりました。
これで、円柱の高さと、底面の半径がわかりましたから表面積を考えていきます。
円柱の表面積は、上底と下底と側面積を足したものです。
(円柱の表面積)=(上底の面積)+(下底の面積)+(側面積)
上底と下底は、同じ面積になりますから
=2×(底面積)+(側面積)
=2×(円の面積)+(長方形の面積)
円の面積を求める式と、長方形の面積を求める式は
(円の面積)=πγ² 、(長方形の面積)=(1辺)×(1辺)
ですから
=2×πγ²+(1辺)×(1辺)
になります。
円の面積は、半径が5cmですから
=2×5×5×π+(1辺)×(1辺)
=50πcm²+(1辺)×(1辺)
長方形の1辺の長さは、円柱の高さで、もう1辺の長さは底面の円の周の長さになります。
円柱の高さは4cm、円周の長さは、まだわかりません。
=50πcm²+4cm×(1辺)
それでは、底面の円周を求めましょう。
(円周)=2πγ
ですから
=2×半径×π
半径は、5cmですから
=2×5×π
=10πcm
=50πcm²+4cm×10πcm
=50πcm²+40πcm²
=90πcm²
になります。
答え 90πcm²
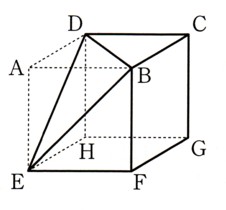
図のような、1辺4cmの立方体から三角錐ABDEを取り除いてできた残りの立方体の
体積を求めてください。
この、問題を解いていく流れを考えていきましょう。
まずは、立方体から三角錐の体積を除いた体積が残りの立体の体積になります。
立方体の体積は、1辺が4cmですから、立方体の体積を求める式は
(立方体の体積)=Sh
=(底面積)×(高さ)
底面積は、正方形ですから、(1辺)×(1辺)=4×4=16?²
=16?²×(高さ)
高さも立方体は同じですから、4cmになります。
=16?²×4cm
=64cm³
これで立方体の体積がわかりました。
次に、取り除く三角錐の体積を考えていきます。
図を見てみるとこの三角錐は、立方体の上底面の対角線DBをつないでます。
ということは、この三角錐の底面は立方体の上底面の半分ということがわかります。
そして三角錐の高さは、立方体の高さにもなりますから。
この三角錐の底面は、立方体の面の半分、高さは立方体と同じ
(立方体の底面の半分)=(三角錐の底面)
(立方体の高さ)=(三角錐の高さ)
三角錐の体積を求める式は、
(三角錐の体積)=1/3×Sh
=1/3×(底面積)×(高さ)
立方体の底面積は、16?²ですから、その半分が三角錐の底面積になります。
16?²÷2=8cm²
高さは、立方体の1辺の長さと同じですから、4cmになります
=1/3×8cm²×4cm
=32/3cm³
になります。
残りの立体の体積を求めるには、
(残りの立体の体積)=(立方体の体積)−(三角錐の体積)
になります
=64cm³−32/3cm³
=192/3cm³−32/3cm³
=160/3cm³
答え 160/3cm³










コメント