中学2年数学 図形の調べ方 図形の合同 確認問題6・解答
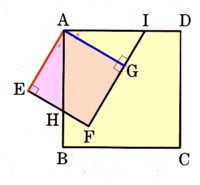
6、図 で、四角形ABCDとAEFGは正方形であり、辺ABと辺EFの交点をH,辺FGの延長と辺ADの交点をIとします。このとき、△AEH≡△AGIを証明してください。
で、四角形ABCDとAEFGは正方形であり、辺ABと辺EFの交点をH,辺FGの延長と辺ADの交点をIとします。このとき、△AEH≡△AGIを証明してください。
答え 
[証明]
△AEHと△AGIにおいて、
仮定により
正方形AEFGですから、4つの辺の長さがすべて等しくなりますから、
AE=AG・・・?
∠AEF=∠AGI・・・?
正方形ABCDですから∠DAB=90°
∠GAHを引くと、∠GAIになります。
∠GAHー∠GAI=90°ー∠GAI・・・?
同じように、正方形AEFGですから、∠EAG=90°
∠GAHを引くと、∠EAHになります。
∠EAGー∠GAI=90°ー∠GAI・・・?
?、?より
∠GAHー∠GAI=∠EAGー∠GAI・・・?
?、?、?より
△AEHと△AGIは、
1つの辺とその両端の角がそれぞれ等しくなる。
よって、
△AEH≡△AGI
になります。







コメント