中学2年数学 式と計算 式の利用 2確認問題2・解答
次の問いに答えてください。
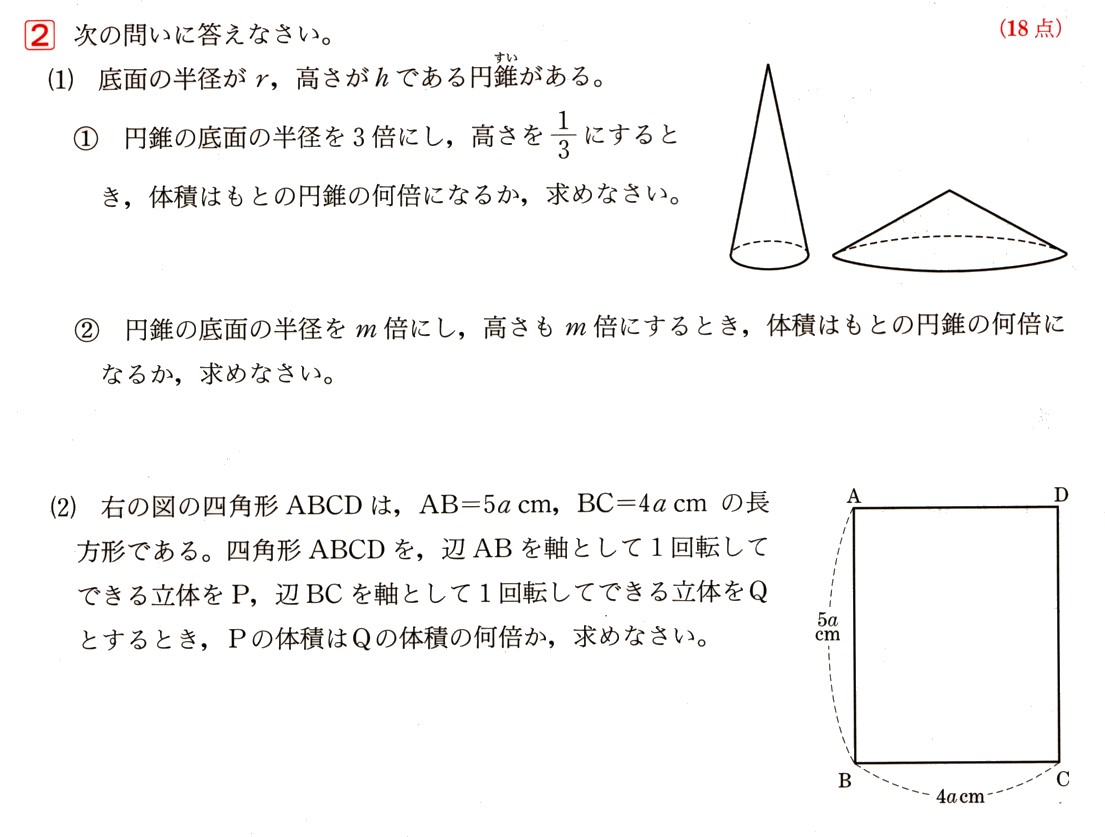
(1)底面の半径がr、高さがhである円錐があります。
?円錐の底面の半径を3倍にし、高さを1/3にするとき、体積は元の円錐の何倍になるか、求めてください。
まずは、円錐の体積を求める式は
底面積の形は円錐ですから円になります。
円の面積の求める式は、(半径)×(半径)×π
になります。
元になる円錐の半径は、r ですから、底面積は、半径が3倍ですから3r になります。
この底面積は、 3r×3r×π ですから
9πr² になります。
高さは h で、この高さを1/3にしますから、1/3×h=h/3 になります。
これで、高さを1/3にして底面の半径を3倍にした円錐の式がわかります。
S=1/3×(底面積)×(高さ)
↓ ↓
9πr² h/3
S=1/3×9πr²×h/3
=πr²h
になります。
元の円錐の体積は、
底面積が、πr²で、高さがhですから
S=1/3×(底面積)×(高さ)
↓ ↓
πr² h
で、πr²h/3 になります。
πr²hを、πr²/3で割れば、何倍かがわかります。
πr²h÷πr²h/3=πr²h×3/πr²h
=3
になります。
答え 3倍
? 円錐の底面の半径をm倍にして、高さもm倍にするとき、体積は元の円錐の何倍になりますか?求めてください。
円錐の体積を求める式は
S=1/3×(底面積)×(高さ)
ですから、半径をm倍にして、高さもm倍にすると
もちろん底面積は円の面積になりますから、
円の面積を求める式は
(半径)×(半径)×π になります。
半径をm倍にしますから
m×(半径)×m×(半径)×π
半径はrですから、
π(mr)² これで底面積がわかりました、高さがhのm倍ですからmhになります。
これを円錐の体積を表す式にあてはめます。
S=1/3×π(mr)²×mh
=πr²m³h/ 3
になります。
元の、円錐の体積は、
S=1/3×πr²×h
=πr²h/ 3
πr²m³h/ 3を、πr²h/ 3で割れば何倍かがわかります。
πr²m³h/ 3 ÷ πr²h/ 3 =πr²m³h/ 3 × 3/πr²h
=m³
になります。
答え m³倍









コメント