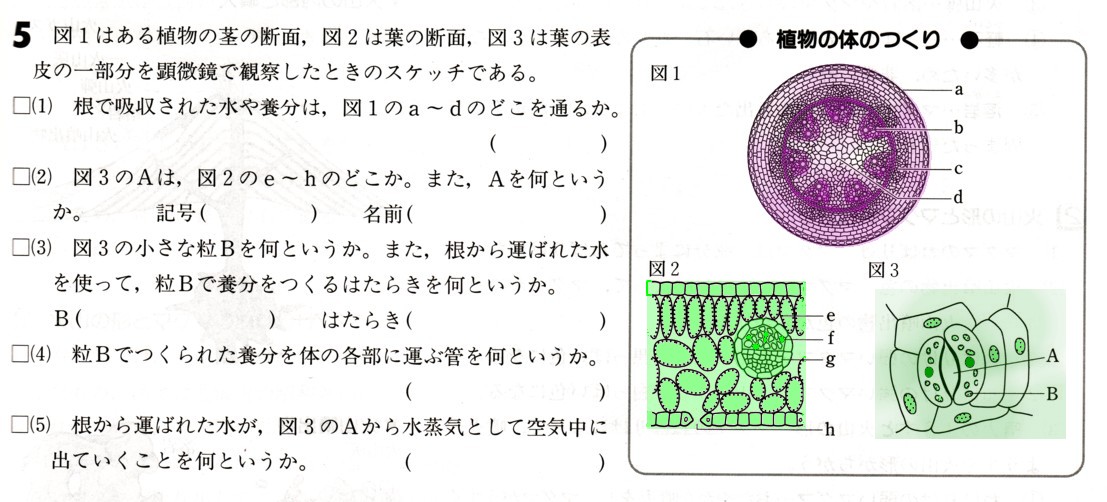
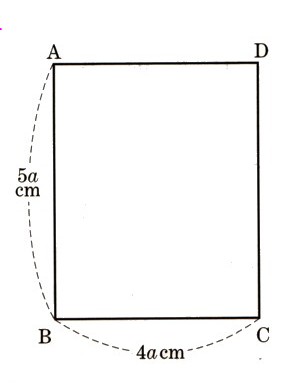
（２）図
の四角形ABCDはAB＝5a(?)、BC＝4a(?)の長方形であります。四角形ABCDを、辺ABを軸として1回転してできる立体をP,辺BCを軸として1回転してできる立体をQとするとき、Pの体積はQの体積の何倍か、求めてください。
まずは、辺ABを軸に1回転してできる立体は、半径4a(?)、高さ5a(?)の円柱になります。この立体がPになります。
辺BCを軸に1回転してできる立体は、半径5a(?)、高さ4a(?)の円柱になります。この立体がQになります。
Pについて考えていきます。
円柱の体積を求める式は
S＝(底面積)×(高さ)
底面積は円ですから、円を求める式は
(円の面積)＝(半径)×(半径)×π
半径は、4a(?)ですから。
4a×4a×π＝16a²π
これで底面積はわかりました。
高さは、5a(?)ですから。
16a²π × 5a ＝80a³π
円柱Pの体積が 80a³π(㎤)とわかりました。
Qについて考えていきます。
円柱の体積を求める式は
S＝(底面積)×(高さ)
底面積は円ですから、円を求める式は
(円の面積)＝(半径)×(半径)×π
半径は、5a(?)ですから。
5a×5a×π＝25a²π
これで底面積はわかりました。
高さは、4a(?)ですから。
25a²π × 4a ＝100a³π
円柱Qの体積が 100a³π(㎤)とわかりました。
たずねているのは、Pの体積は、Qの体積の何倍になるかですから。
PをQで割れば、何倍かがわかります。
80a³π÷100a³π＝80a³π ／ 100a³π
＝4／5
答え 4／5 倍
コメント