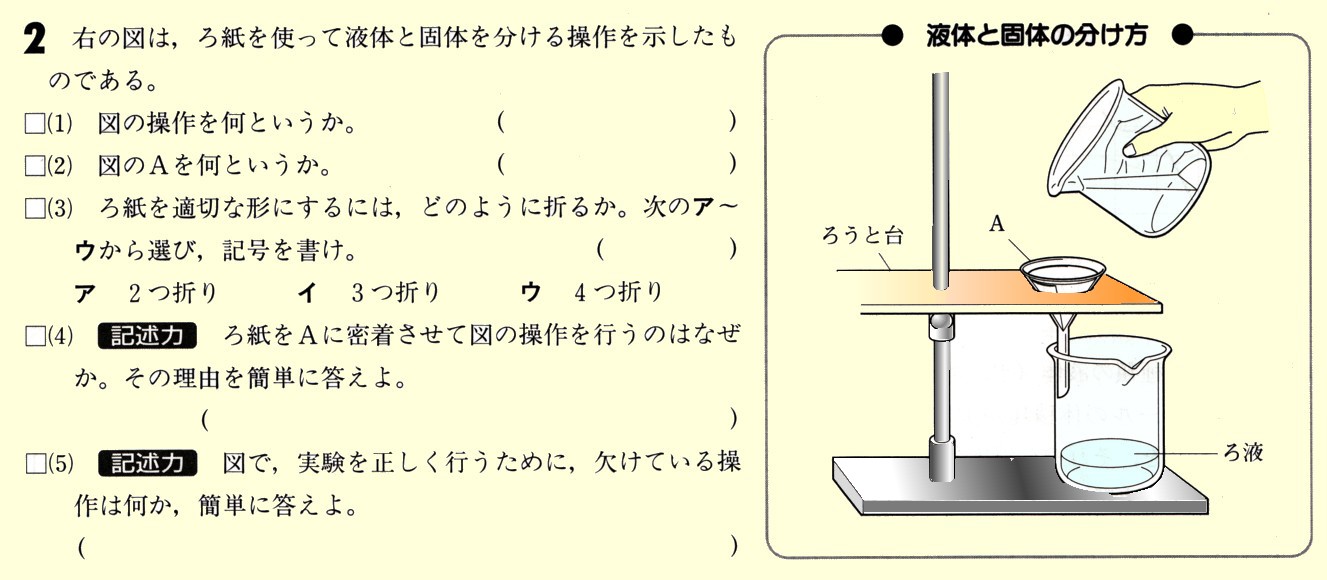
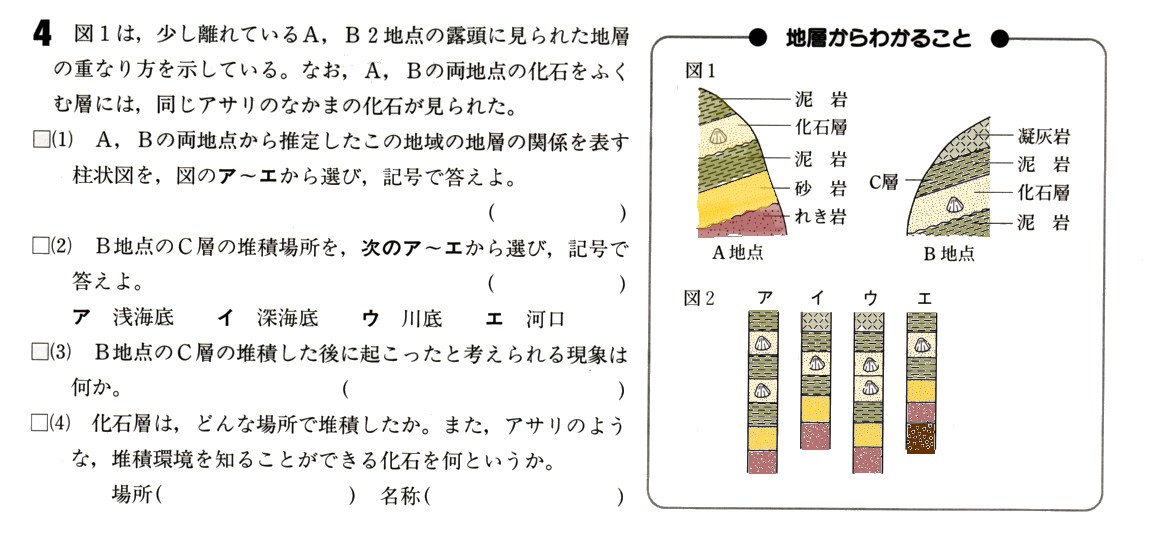
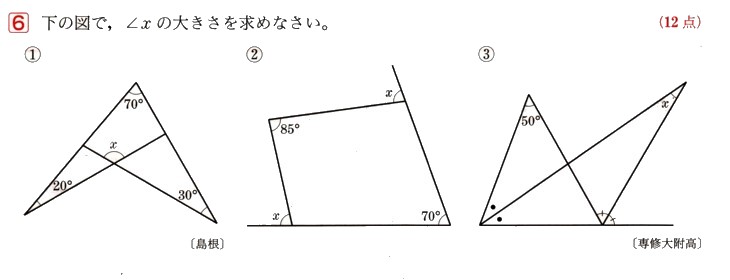
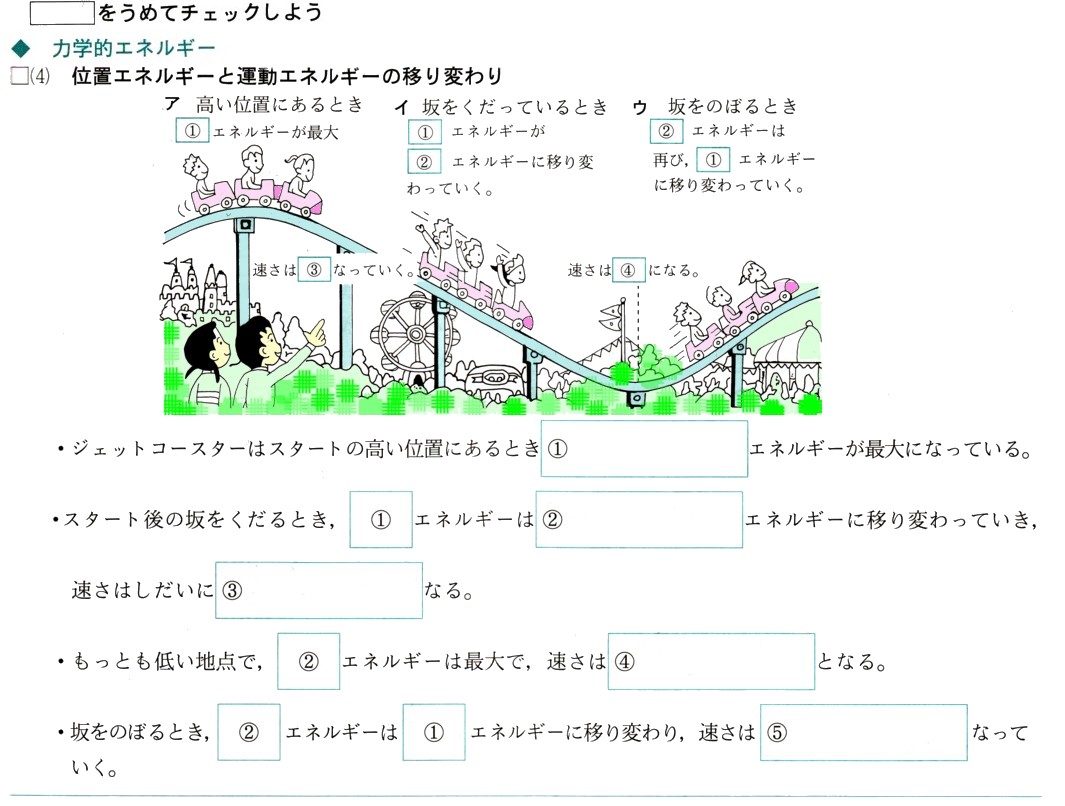
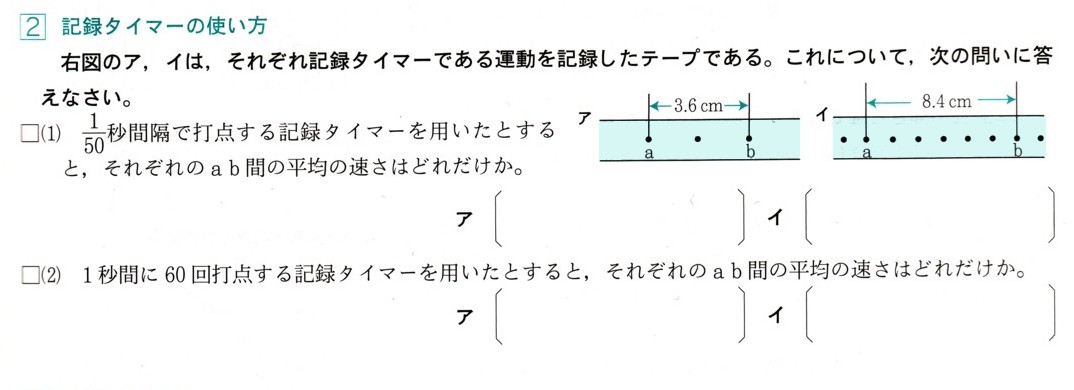
中学1年数学 円とおうぎ形の計算 練習問題2 解答・解説
次のおうぎ形の弧の長さと面積を求めてください。
(おうぎ形の弧の長さ)=2πγ×a/360
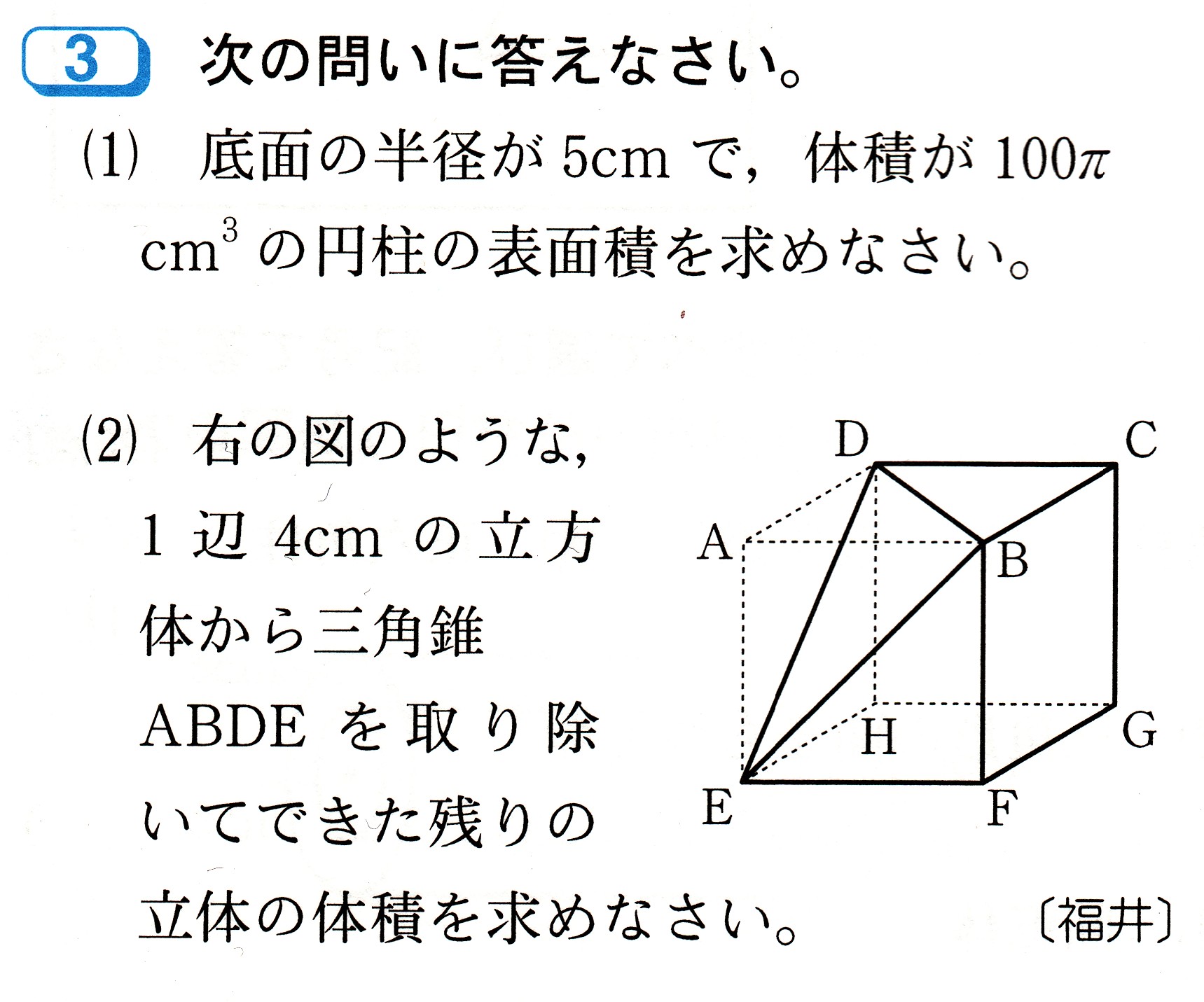
=2×π×半径×(中心角)/360
(おうぎ形の面積)=πγ²×a/360
=π×半径×半径×(中心角)/360
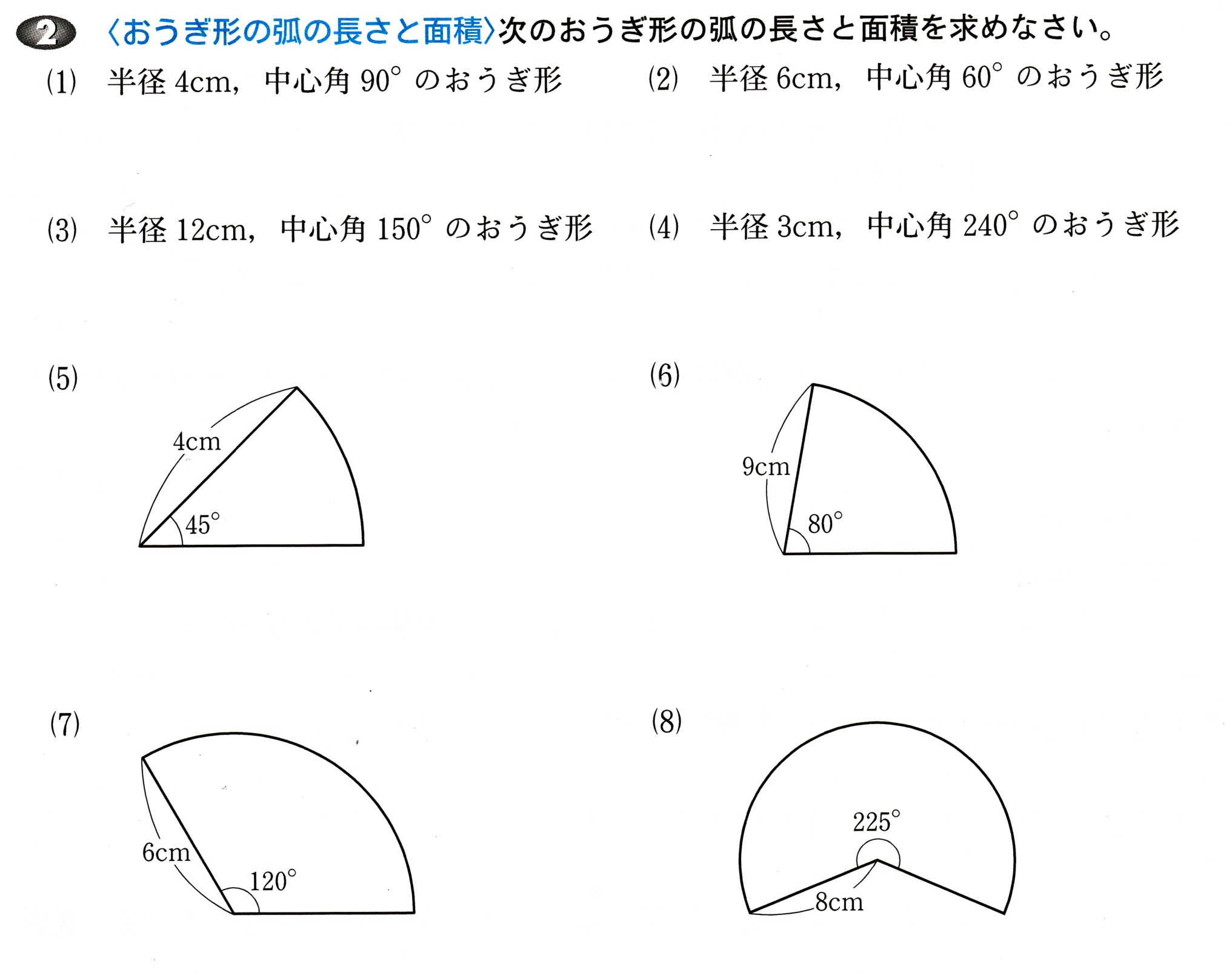
(1)半径4cm、中心角90゜のおうぎ形
(おうぎ形の弧の長さ)=2πγ×a/360
ですから、
(おうぎ形の弧の長さ)=2×π×半径×(中心角)/360
=2×π×4cm×90゜/360゜
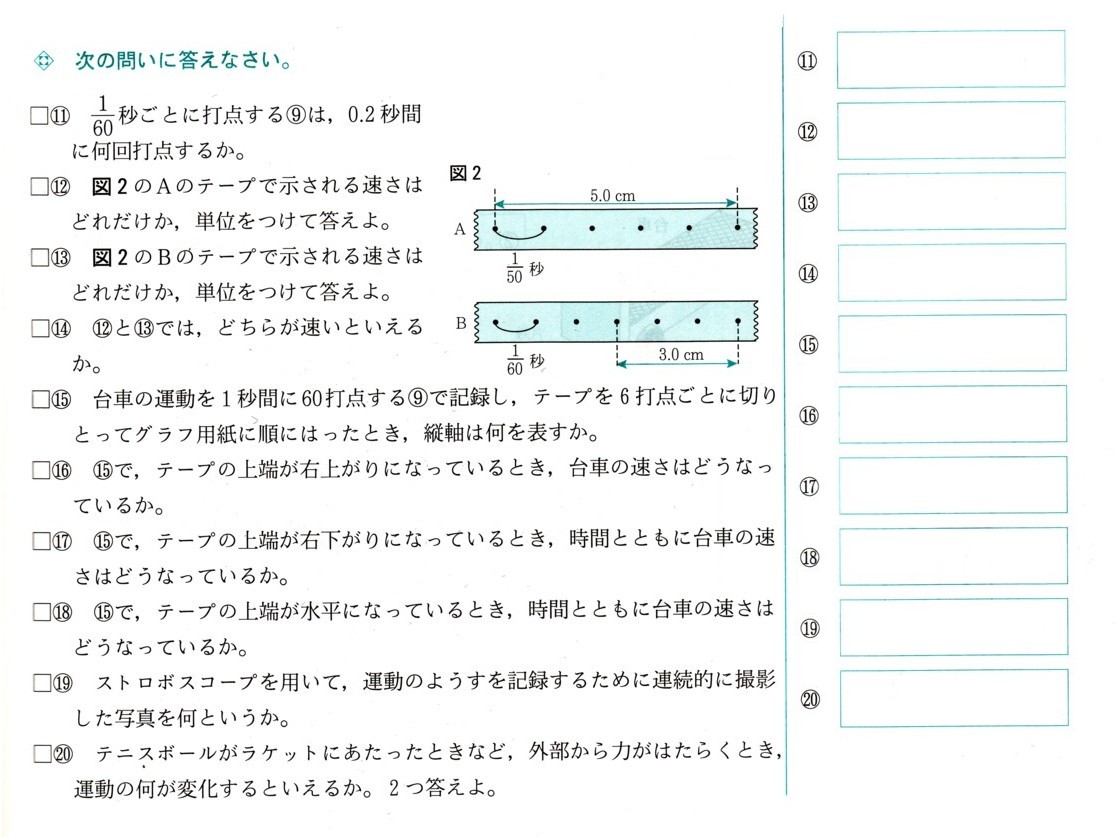
=8π1/4
=2π(cm)
(おうぎ形の面積)=πγ²×a/360
ですから、
(おうぎ形の面積)=π×半径×半径×(中心角)/360
=π×4cm×4cm×90゜/360゜
=16π1/4
=4π(cm²)
答え 弧の長さ 2π(cm) 、おうぎ形の面積 4π(cm²)
(2)半径6cm、中心角60゜のおうぎ形
(おうぎ形の弧の長さ)=2πγ×a/360
ですから、
(おうぎ形の弧の長さ)=2×π×半径×(中心角)/360
=2×π×6cm×60゜/360゜
=12π1/6
=2π(cm)
(おうぎ形の面積)=πγ²×a/360
ですから、
(おうぎ形の面積)=π×半径×半径×(中心角)/360
=π×6cm×6cm×60゜/360゜
=12π1/6
=2π(cm²)
答え 弧の長さ 2π(cm) 、おうぎ形の面積 2π(cm²)
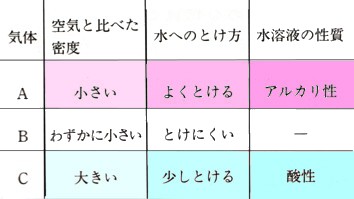
(3)半径12cm、中心角150゜のおうぎ形
(おうぎ形の弧の長さ)=2πγ×a/360
ですから、
(おうぎ形の弧の長さ)=2×π×半径×(中心角)/360
=2×π×12cm×150゜/360゜
=24π5/12
=10π(cm)
(おうぎ形の面積)=πγ²×a/360
ですから、
(おうぎ形の面積)=π×半径×半径×(中心角)/360
=π×12cm×12cm×150゜/360゜
=144π5/12
=60π(cm²)
答え 弧の長さ 10π(cm) 、おうぎ形の面積 60π(cm²)
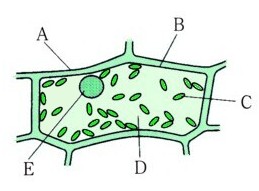
(4)半径3cm、中心角240゜のおうぎ形
(おうぎ形の弧の長さ)=2πγ×a/360
ですから、
(おうぎ形の弧の長さ)=2×π×半径×(中心角)/360
=2×π×3cm×240゜/360゜
=6π2/3
=4π(cm)
(おうぎ形の面積)=πγ²×a/360
ですから、
(おうぎ形の面積)=π×半径×半径×(中心角)/360
=π×3cm×3cm×240゜/360゜
=9π2/3
=6π(cm²)
答え 弧の長さ 4π(cm) 、おうぎ形の面積 6π(cm²)
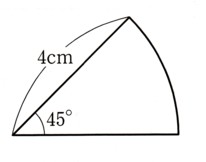
(5)図
(おうぎ形の弧の長さ)=2πγ×a/360
ですから、
(おうぎ形の弧の長さ)=2×π×半径×(中心角)/360
=2×π×4cm×45゜/360゜
=8π1/8
=π(cm)
(おうぎ形の面積)=πγ²×a/360
ですから、
(おうぎ形の面積)=π×半径×半径×(中心角)/360
=π×4cm×4cm×45゜/360゜
=16π1/8
=2π(cm²)
答え 弧の長さ π(cm) 、おうぎ形の面積 2π(cm²)
(6)図
(おうぎ形の弧の長さ)=2πγ×a/360
ですから、
(おうぎ形の弧の長さ)=2×
π×半径×(中心角)/360
=2×π×9cm×80゜/360゜
=18π2/9
=4π(cm)
(おうぎ形の面積)=πγ²×a/360
ですから、
(おうぎ形の面積)=π×半径×半径×(中心角)/360
=π×9cm×9cm×80゜/360゜
=81π2/9
=18π(cm²)
答え 弧の長さ 4π(cm) 、おうぎ形の面積 18π(cm²)
(7)図
(おうぎ形の弧の長さ)=2πγ×a/360
ですから、
(おうぎ形の弧の長さ)=2×π×半径×(中心角)/360
=2×π×6cm×120゜/360゜
=12π1/3
=4π(cm)
(おうぎ形の面積)=πγ²×a/360
ですから、
(おうぎ形の面積)=π×半径×半径×(中心角)/360
=π×6cm×6cm×120゜/360゜
=36π1/3
=12π(cm²)
答え 弧の長さ 4π(cm) 、おうぎ形の面積 12π(cm²)
(8)図
(おうぎ形の弧の長さ)=2πγ×a/360
ですから、
(おうぎ形の弧の長さ)=2×π×半径×(中心角)/360
=2×π×8cm×225゜/360゜
=16π5/8
=10π(cm)
(おうぎ形の面積)=πγ²×a/360
ですから、
(おうぎ形の面積)=π×半径×半径×(中心角)/360
=π×8cm×8cm×225゜/360゜
=64π5/8
=40π(cm²)
答え 弧の長さ 10π(cm) 、おうぎ形の面積 40π(cm²)











コメント