中学2年数学 平面図形 まとめテスト4・解答
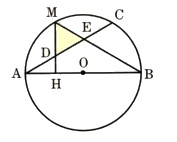
4、図 のように、円の直線ABの一端Aから弦ACをひき、弧ACの中点をMとします。点MからABにおろした垂線をMHとし、ACと、MH、MBの交点をそれぞれD、Eとするとき、次の問いに答えてください。
のように、円の直線ABの一端Aから弦ACをひき、弧ACの中点をMとします。点MからABにおろした垂線をMHとし、ACと、MH、MBの交点をそれぞれD、Eとするとき、次の問いに答えてください。
 のように、円の直線ABの一端Aから弦ACをひき、弧ACの中点をMとします。点MからABにおろした垂線をMHとし、ACと、MH、MBの交点をそれぞれD、Eとするとき、次の問いに答えてください。
のように、円の直線ABの一端Aから弦ACをひき、弧ACの中点をMとします。点MからABにおろした垂線をMHとし、ACと、MH、MBの交点をそれぞれD、Eとするとき、次の問いに答えてください。(1)△DEMは二等辺三角形になることを証明してください。
答え
〔証明〕
まずは、 ∠ABM=χとします。
 そうすると、△HMBにおいて
そうすると、△HMBにおいて ∠HMB=180°−(90°+χ)・・・①
になります。
また、弧AM=弧MCになりますから、
円周角の定理により
∠MAC=∠ABM=χ
となります。
さらに、ABは円の直径になりますから

∠AMB=90°
になり,△MAEにおいて、
 ∠AEM=180°ー(90°+χ)
∠AEM=180°ー(90°+χ) =180°ー90°ーχ
=90°ーχ
になり、
∠DEM=90°−χ・・・②
①、②より
∠DME=∠DEM
よって、
△DEMは二等辺三角形になります。
(2)点Dは線分AEの中点であることを証明してください。
 まずは、△AMHと△AMBを考えます。
まずは、△AMHと△AMBを考えます。 ①より、

∠AMD=90°−(90°−χ)
=90°ー90°+χ<
/span>
=χ
また、∠MAD=χ
になりますから、
∠AMD=∠MAD
となり、△MADは二等辺三角形になります。
二等辺三角形の2つの辺DAとDEは等しくなりますから
DA=DE・・・③
一方、(1)よりDA=DE・・・④
ですから
③、④より
DA=DE
となり、点Dは線分AFの中点になります。









コメント