中学2年数学 1次関数 1次関数のグラフと式の求め方 確認問題2・解答
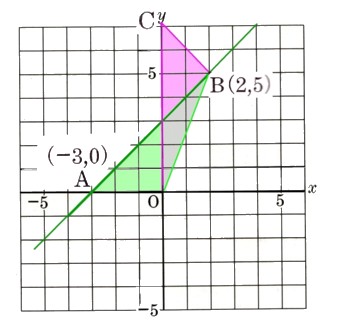
2、次の図 で、Oは原点、点A,Bの座標はそれぞれ(−3,0)、(2,5)である。また、点Cはy座標は正である。△AOBと△COBの面積が等しいとき、次の問いに答えて下さい。
で、Oは原点、点A,Bの座標はそれぞれ(−3,0)、(2,5)である。また、点Cはy座標は正である。△AOBと△COBの面積が等しいとき、次の問いに答えて下さい。
(1)2点A,Bを通る直線の式を求めて下さい。
比例のグラフですから、1次関数の式にあてはまります。
y=aχ+b
(χ、y)=(−3,0)、(2,5)
連立方程式をつくります。
(0)=a(−3)+b
{
(5)=a(2)+b
−3a+b=0
{
2a+b=5
−3a+b=0
−) 2a+b=5
−5a =−5
a=1
2a+b=5 に a=1 を代入します。
2(1)+b=5
2+b=5
b=5−2
b=3
a=(傾き)=1、b=(切片)=3
y=aχ+b
y=(傾き)χ+(切片)
y=χ+3
になります。
答え y=χ+3
面積は同じですから
△AOB=△COB
△AOB の面積は、
底辺がO~A 3cm
高さは B点(2,5)のyですから 5cm
三角形の面積は
(底辺)×(高さ)÷2=(三角形の面積)
(3cm)×(5cm)÷2=(△AOBの面積)
(△AOBの面積)=7.5㎠
(△AOBの面積)=7.5㎠=(△COBの面積)
(△COBの面積)=7.5㎠=(底辺)×(高さ)÷2
点B(2,5)=(χ、y)
y=△COBの高さになりますから(χ、y)=(2,5)
△COBの高さは、2cmになります。
(△COBの面積)=7.5㎠=(底辺)×(高さ)÷2
(△COBの面積)=7.5㎠=(底辺)×(2cm)÷2
(底辺)をχとして式をつくります。
7.5=2χ/2
15=2χ
2χ=15
χ=7.5
点C の座標は、χ座標は0で、y座標は7.5 になりますから、
点C( 0 , 7.5 )になります。
答え ( 0 , 7.5 )=(χ、y)









コメント