中学2年数学 平面図形 三角形の性質 確認問題8・解答
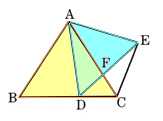
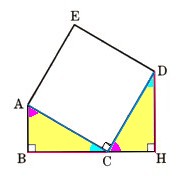
8、∠B=90°である直角三角形ABCの外側に、ACを一辺とする正方形ABCDをつくり、DからBCの延長に垂線DHを引きます。このとき、BC=DHであることを証明してください。

答え
〔証明〕
△ABCと△CDHにおいて
仮定より
四角形ABCDは正方形ですから4つの辺はそれぞれ等しくなりますから
AC=CD・・・①
∠ABC(90°)=∠CHD(90°)・・・②
点Cの部分を考えます。
∠ACB=180°ー(∠ACD+∠DCH)
△CDHの部分を考えます。
∠CDH=180°ー(∠DHC+∠DCH)
∠ACDと∠DHCは直角ですから、
∠ACD=∠DHC
になりますから、
∠ACB=∠CDH・・・③
①、②、③より
直角三角形は、斜辺と1つの鋭角がそれぞれ等しくなりますから
△ABC≡△CHD
になります。
合同な三角形の対応する辺はそれぞれ等しくなりますから
BC=HD
になります。








コメント