中学3年数学 三平方の定理の利用 練習問題3・解答
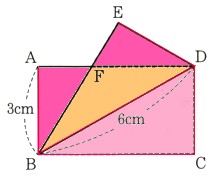
3、次の図 のように、長方形ABCDを対角線BDで折り重ねて、点Cが移動した点をEとします。
のように、長方形ABCDを対角線BDで折り重ねて、点Cが移動した点をEとします。
ADとBEの交点をFとしたとき、AB=3cm、BD=6cmとします。
次の問いに答えてください。
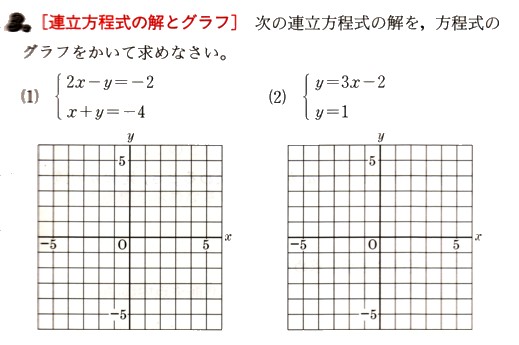
(1)∠FDEの大きさを求めてください。
△EDFと△ABFは合同な三角形になります。
△EDF≡△ABF
△ABDと△AFBは相似の関係になりますから、
△ABD∽△AFB
次に△ABDと△CDBは合同な三角形になりますから、
△CDBの斜辺をBD=6cm、底辺をCD=3cm、高さをBCと考え、
同じ直角三角形を2つ合わせると、3辺の長さが同じ三角形になりますから、
この三角形は正三角形になります。正三角形の1つの内角は60゜ですから、
∠BDC=60゜ということがわかります。
(△CDB≡△ABD)∽(AFB≡EDF)となります。
これにより、
∠BDC=60゜=∠DBA=∠BFA=∠DFE
となります。
∠DBC=180゜−(∠DCB+∠BDC)
∠DCB=90゜
∠BDC=60゜
∠DBC=180゜−(90゜+60゜)
∠DBC=30゜
(△CDB≡△ABD)∽(AFB≡EDF)ですから
∠DBC=30゜=∠BDA=∠FBA=∠FDE
答え 30゜
(2)DFの長さを求めてください。
DFの長さは、ADの長さからAFのながさをひけばわかります。
ADの長さは、直角三角形ADBの直角を挟む長い辺になります。
辺AB(直角を挟む短い辺)=3cm
辺AD(直角を挟む長い辺)=χ?
辺BD(斜辺)=6cm
三平方の定理を利用します。
(直角を挟む長い辺)²+(直角を挟む短い辺)²=(斜辺)²
χ²+3²=6²
χ²+9=36
χ²=36−9
χ²=27
χ=±√27=±3√3(χは+ですから)
χ=3√3?
辺AD=3√3?
△ABD∽△AFBですから、
AB:AD=AF:AB
AB=3cm
AD=3√3cm
AF=χ?
< span style="background-color: #ffcc99;">3:3√3=χ:3
3×3=3√3×χ
9=3√3χ
9/3√3=3√3χ/3√3
χ=3/√3
χ=3√3/√3×√3
χ=3√3/3=√3
AF=√3?
AD−AF=DF
AD=3√3cm
AF=√3?
3√3−√3=2√3
答え 2√3?









コメント