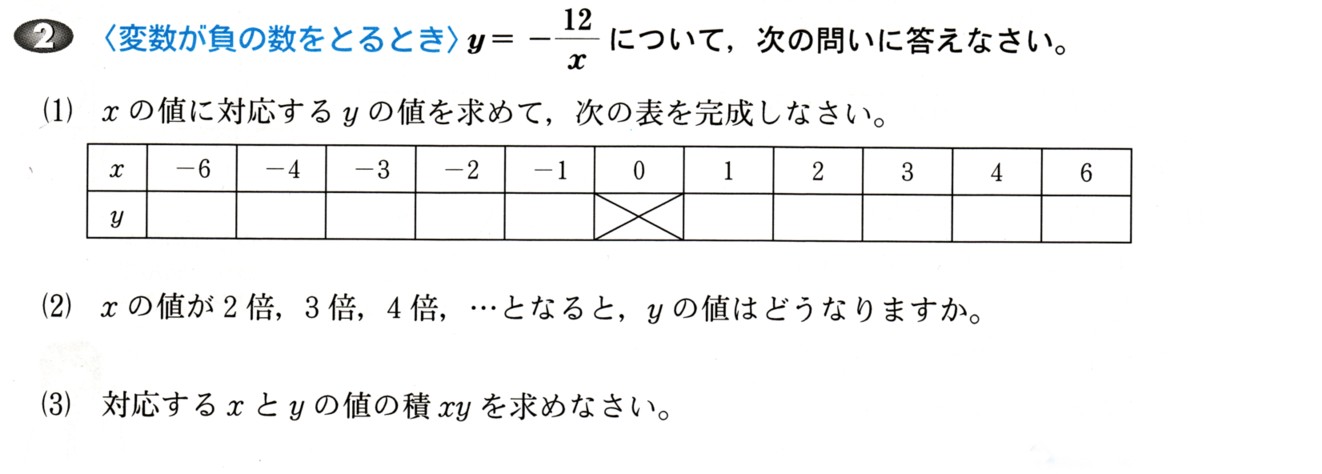
中学3年数学 図形と相似 練習問題4・解答
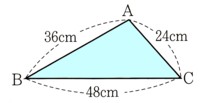
4、図 のような△ABCがあります。この三角形と相似で、1辺が12?の三角形を作図するとき、次の問いに答えてください。
のような△ABCがあります。この三角形と相似で、1辺が12?の三角形を作図するとき、次の問いに答えてください。
(1)三角形は全部でいくつかけますか?
それぞれの辺AB,BC,CAを12cmの辺で考えると、
?ABが12?ならば12/36で1/3、すべての辺の長さを1/3にすれば相似な三角形ができます。
?BCが12cmならば12/48で1/4、すべての辺の長さを1/4にすれば相似な三角形ができます。
?CAが12cmならば12/24で1/2、すべての辺の長さをにすれば相似な三角形ができます
答え 3つ
(2)辺ACに対応する辺の長さを12?にする三角形を△DEFとし、辺ACに対応する辺をDFとすれば、辺DEの長さは何cmになりますか?
(1)でそれぞれ対応する長さは1/2になりますから、AC:DF=2:1、AB:DE=2:1
DEの長さは36/2=18
答え 18cm
(3)作図できる三角形のうちで、最も小さいものを、△PQRとし、△ABC∽△PQRであるとき、△PQRの三辺の長さを求めてください。
最も小さい相似の三角形を作図するためには、3つの辺で一番長い辺を12cmにすれば3つの辺が一番小さくなりますから、
辺AB=36?
辺BC=48?
辺CA=24?
辺BCを12cmにすればいいとわかります。
12/48=1/4
36÷4=9?
24÷4=6?
辺AB=辺PQ 9cm
辺CA=辺RP 6cm
になります。
答え 辺PQ=9cm、辺QR=12cm、辺RP=6cm








コメント