中学3年数学 三平方の定理の利用 練習問題2・解答
2、次の問いに答えてください。
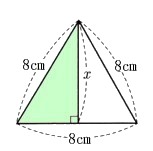
(1) 1辺の長さが8cmの正三角形の面積を求めてください。
1辺の長さが8cmの正三角形の面積を求めてください。
頂角から底辺に垂線を引いた線(高さ)を求めれば正三角形の面積がわかります。
斜辺の長さを8cm
直角を挟む1つの辺の長さを4cm
もう一つの辺の長さをχ?とします。
正三角形 ですから1つの角が60゜になりますから、90゜、60゜、30゜になります。
この場合の比率は1:2:√3=(短い辺の長さ):(斜辺の長さ):(長い辺の長さ)
(短い辺の長さ)は4cm になり。
(斜辺の長さ)を8? になり。
(長い辺の長さ)をχ? で考えます。
2 :√3=(斜辺の長さ):(長い辺の長さ)
2 :√3=8:χ
2 ×χ=√3×8
2 χ=8√3
χ =4√3
χ はこの正三角形の高さになりますから4√3?になります
三角形の面積 は
底辺=8cm 、高さ4√3cm
8 ×4√3×1/2=32√3/2=16√3
正三角形の面積 は16√3㎠とわかります。
答え 16√3㎠
(2) 1辺の長さが4cm、1つの対角線の長さが4cmのひし形の面積を求めてください。
1辺の長さが4cm、1つの対角線の長さが4cmのひし形の面積を求めてください。
ひし形は4つの辺の長さが等しく なりますから、対角線の長さが4cmということは、
正三角形×2 となります。
正三角形の半分の直角三角形はその他の1つの角が60゜になりますから、
比率は1:2:√3=(短い辺の長さ):(斜辺の長さ):(長い辺の長さ)
になります。
(短い辺の長さ)=2cm
(斜辺の長さ)=4cm
(長い辺の長さ)=χ? として考えます。
2 :√3=(斜辺の長さ):(長い辺の長さ)
2 :√3=4:χ
2 ×χ=√3×4
2 χ=4√3
χ =2√3
OB の長さが2√3?とわかりましたから、BDの長さは2√3×2=4√3
ひし形の面積の求め方は(対角線)×(対角線)×1/2
対角線AC=4cm
対角線BD=4√3?
4 ×4√3×1/2=16√3/2=8√3
答え 8√3?
(3) 対角線が6cm、8cmであるひし形の1辺の長さを求めてください。
対角線が6cm、8cmであるひし形の1辺の長さを求めてください。
ひし形ですから二等辺三角形が2つあると考えます。
そしてこの二等辺三角形は2つの直角三角形からできています。
(短い辺の長さ)=3cm
(斜辺の長さ)=χ?
(長い辺の長さ)=4cm
直角三角形の辺の長さは、
(直角を挟む長い辺の長さ)²+(直角を挟む短い辺の長さ)²=(斜辺の長さ)²
4²+3²=χ²
16 +9=χ²
25=χ²
χ =±5(χは+になりますから)
斜辺の長さは5cm になります。
答え 5cm
(4) 等しい辺の長さが7cm、底辺の長さが10cmの二等辺三角形の面積を求めてください。
等しい辺の長さが7cm、底辺の長さが10cmの二等辺三角形の面積を求めてください。
三角形の面積を求めるための高さがさわかりませんから、
頂角から底辺に向けて垂線を引きます。
そうすると、2つの直角三角形になります。
この直角三角形の高さを5cm
斜辺を7cm
底辺をχ?として考えます。
直角三角形の辺の長さは、
(直角を挟む長い辺の長さ)²+(直角を挟む短い辺の長さ)²=(斜辺の長さ)²
5²+χ²=7²
25+χ²=49
χ²=49−25
χ²=24
χ=±√24(χは+ですから)
χ=√24=2√6
χは二等辺三角形の高さになりますから2√6?、底辺の長さが10?になります。
10×2√6×1/2=20√6/2=10√6
答え 10√6㎠












コメント