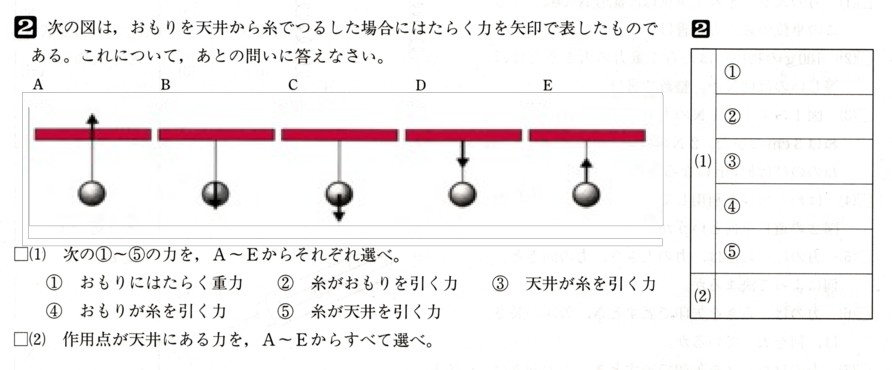
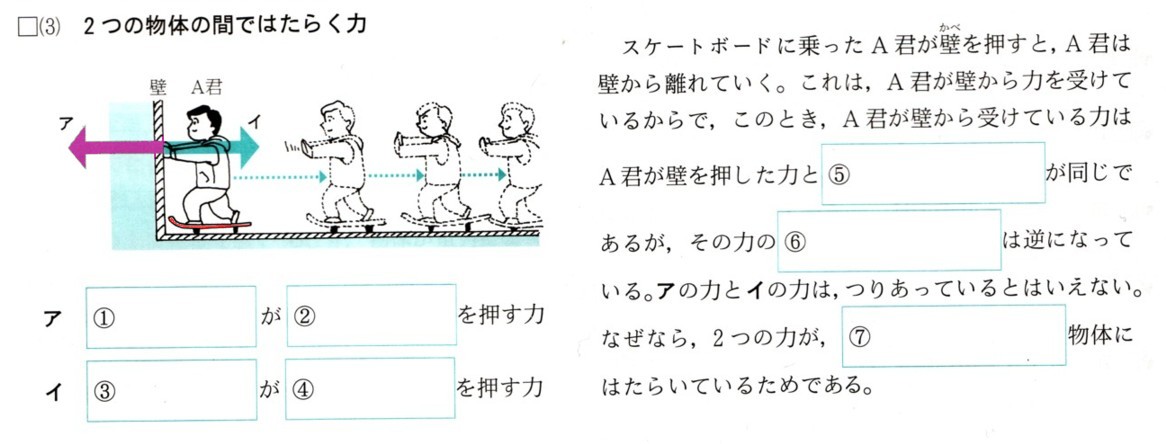
練習問題2(方程式の利用3)解等・解説

1個120円のりんごと1個80円のみかんを合わせて10個買ったら、代金が

　960円になりました。りんごχ個買ったとして、次の問いに答えてください。

　(1)みかんを買った個数を記号の式で表してください。

　　　　　りんごの数をχで表します

　　たずねているのは、みかんの数になります。

　　　りんごの数がχで、総数は10個ですから

　　　総数からりんごの数をひけば、みかんの数がわかります。

　　　(みかんの数)＝(総数−りんごの数)

　　総数は10個ですから、

　　　(みかんの数)＝(１０−りんごの数)

　　りんごの数＝χですから

　　　(みかんの数)＝(１０−χ(個))

　　答え　１０−χ(個)

　(2)χについての方程式をつくってください。

　　χについてとは、　りんごの数についてということになります。

　　　りんごの数＝χで1次方程式を作ります

　　　　整理してみましょう

　　わかっているのは、

　　　　　りんご1個の値段　　　　120(円)

　　　　　みかん1個の値段　　　　　80(円)　

　　　　　　10個、買う

　　　　　　そのときの代金は　　　960(円)

　(合計金額)＝(りんごの値段)+(みかんの値段)

　(りんごの値段)は、(りんご1個の値段)×(りんごの数)

　(りんごの値段)＝　　　120(円)　　　×　χ　

　　　　　　　　＝　　120χ(円)

　(みかんの値段)は、(みかん1個の値段)×｛(総数１０こ)−(りんごの数)｝
　　　　　　　　　　　　　　　　　　　　　　　　　　‖
　　　　　　　　　　　　　　　　　　　　　　　(みかんの数)

　　(みかんの値段)＝　　　80(円)　　　×　　　(10−χ)

　　(合計金額)＝(りんごの値段)+(みかんの値段)

　　　960(円)＝　120χ(円)　　＋80(10−χ)(円)

　　　答え　960＝120χ＋80(10−χ)

　(3)りんごとみかんをそれぞれ何個ずつ買ったか、求めてください。

　　　上の方程式の解が、りんごの数になります、

りんごの数がわかれば、10個からりんごの数をひけばみかんの数がわかります。

　　りんごの数は、χです。

　　　それでは解いていきましょう

　　　　960＝120χ＋80(10−χ)

　　まずは、カッコをはずします

　　　　960＝120χ＋800−80χ

　　右辺の800を移項して符号を変えます

　　　960−800＝120χ−80χ

　　　　　160＝40χ

　　　　左辺と右辺を変えます

　　　　　40χ＝160

　　　両辺に1/40をかけます

　　　　　　1/40×40χ＝1/40×160

　　　　　　　　　χ＝4

　　　りんごの数が4個とわかりました。

　　りんごとみかんの総数は10個ですから、10個からりんごの4個をひけば

　　みかんの数がわかります

　　　　(りんごとみかんの総数)−(りんごの数)＝(みかんの数)

　　　　　　　10個　　　　　　−　　4個　　　＝　6個

　　　　みかんの数は6個になります。

　　　答え　りんご　4個　、みかん　6個