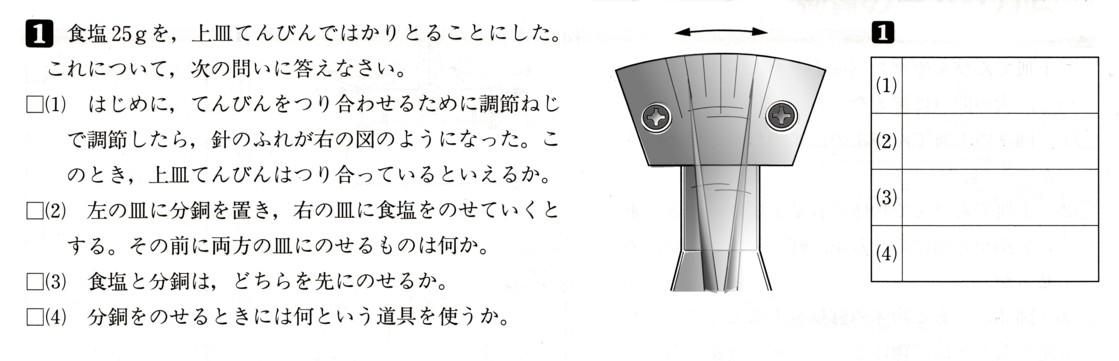
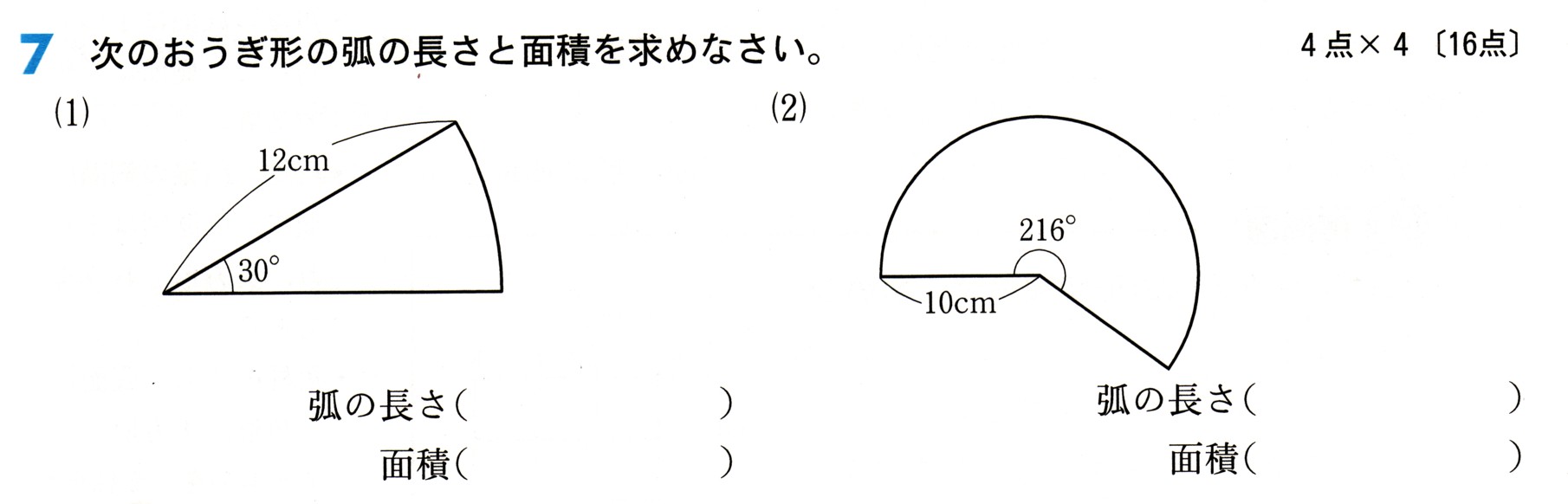
中学3年数学 二次方程式 3確認問題2・解答
2、次の問いに答えてください。
(1)二次方程式χ²+3aχーaー5=0 の解の1つが4のとき、aの値を求めてください。また、他の解を求めてください。
χ²+3aχーaー5=0にχ=4を代入します。
(4)²+3a4ーaー5=0
16+12aーaー5=0
11+11a=0
11a=−11
a=−1
χ²+3aχーaー5=0に a=−1を代入します。
χ²ー3χ+1−5=0
χ²ー3χー4=0
因数分解をします。
χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけてー4 、たしてー3になる2つの数は
1×(−4)=−4 、1+(−4)=−3
χ²ー3χー4=(χ+1)(χー4)
(χ+1)(χー4)=0
A×B=0ならば、A=0 または B=0 になります。
ですから、
χ+1=0、χー4=0
χ=−1、χ=4
答え a=−1、χ=−1
(2)二次方程式 χ²−2χー15=0の負の方の解が、二次方程式 χ²+aχー2a+6=0の解の1つになっています。このときaの値を求めてください。
χ²−2χー15=0
因数分解をします。
χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけてー15 、足してー2になる2つの数は
3×(−5)=(−15) 、3+(−5)=−2
χ²−2χー15=(χ+3)(χー5)
(χ+3)(χー5)=0
A×B=0 ならば A=0 または B=0 になります。
ですから、
χ+3=0、χー5=0
χ=−3、χ=5
負の方の解を χ²+aχー2a+6=0 に代入します。
(−3)²ー3aー2a+6=0
9ー3aー2a+6=0
ー5a=ー6ー9
−5a=−15
a=3
答え a=3
(3)二次方程式 χ²+3χ+a=0の1つの解がー5で、他の解が、
bχーy=9
χ、yについての連立方程式{ のχの解と同じになります。
2χ+3y=−5
このとき、a、bの値を求めてください。
χ²+3χ+a=0 に χ=−5を代入します。
(−5)²+3×(−5)+a=0
25ー15+a=0
a=−25+15
a=−10
χ²+3χ+a=0に a=−10 を代入します。
χ²+3χ−10 =0
因数分解をします。
χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけてー10 、足して3になる2つの数は
5×(−2)=−10 、5+(−2)=3
χ²+3χ−10=(χ+5)(χー2)
(χ+5)(χー2)=0
A×B=0 ならば A=0 または B=0 になります。
ですから、
χ+5=0、χー2=0
χ=−5、χ=2
bχーy=9
{ にχ=2を代入します。








コメント