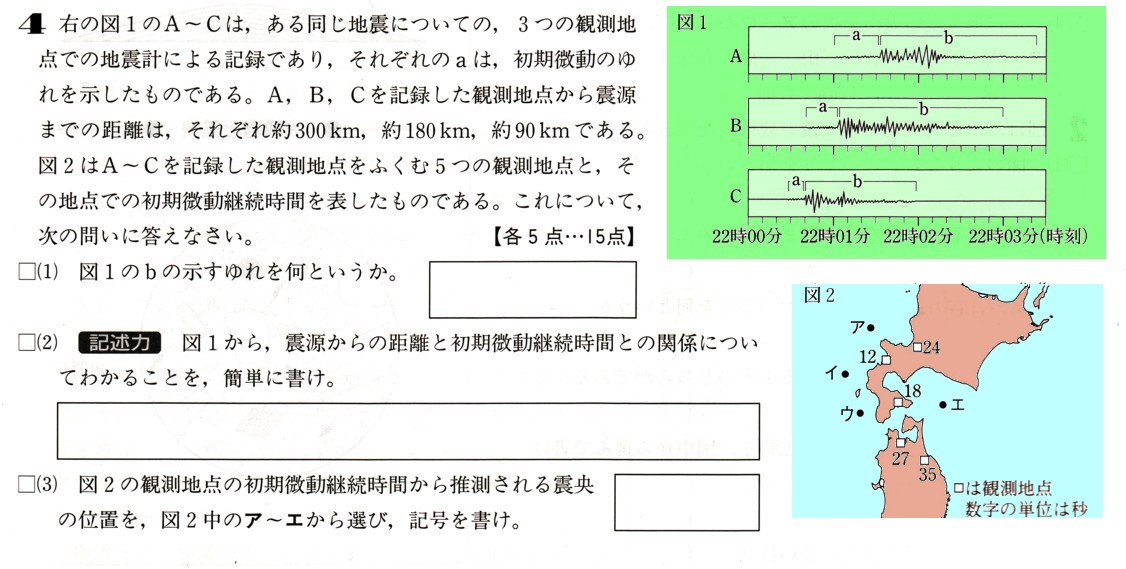
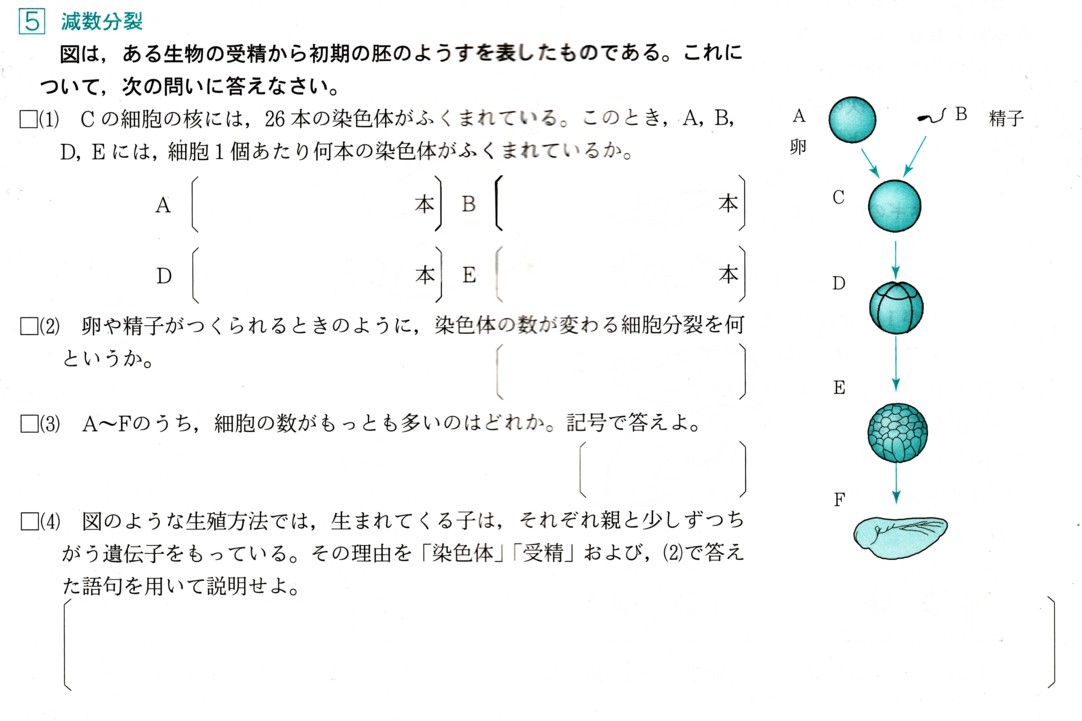
中学3年数学 図形と相似 平行線と線分の比 2確認問題2・解答
2、次の図 のように、△ABCがあります。辺AB,ACの中点をそれぞれD,Eとして、
のように、△ABCがあります。辺AB,ACの中点をそれぞれD,Eとして、
辺BCを1:2に分ける点をFとします。また、線分CDと線分EFとの交点をGとします。
CG=6cmのとき、線分GDの長さを求めてください。

まずは、DEに補助線を引きます。
この補助線は、中点連結定理でBCの半分の長さになりますから
DE//BCで、DE=1/2BC になります。
そうすると、BF:FC=1:2 ですから、
BF=1/3BC、FC=2/3BC になります。
DE//BC ですから、
△GED∽△GFC になります。
この△GED:△GFCはDE:FC=1/2:2/3 ですから
△GED:△GFC=1/2:2/3=3/6:4/6=3:4
となります。
GC=6cmですから
DG:GC=3:4
DG:6=3:4
DG×4=6×3
4DG=18
DG=18/4=9/2
答え 9/2cm









コメント