中学3年数学 三平方の定理の利用 練習問題9・解答
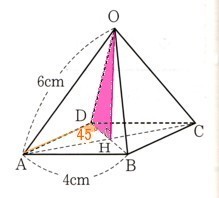
9、図 のような正四角錘O−ABCDがあります。底面は、1辺4cmの正方形で、
のような正四角錘O−ABCDがあります。底面は、1辺4cmの正方形で、
他の辺の長さはすべて6?になります。底面の対角線の交点をHとするとき、
次の問いに答えてください。
(1)この立体の体積を求めてください。
△AHDで考えます。
△AHDは∠ADH=45゜の直角二等辺三角形になりますから、
(1辺):(1辺):(斜辺)=1:1:√2
斜辺をAD=4?
1辺をχ?として考えます。
(1辺):(斜辺)=1:√2=χ:4
1×4=χ×√2
4=χ√2
4/√2=χ√2/√2
4√2/√2×√2=χ
4√2/2=χ
2√2=χ
DH=2√2?
△ODHで考えます。
△ODHは直角三角形ですから、三平方の定理を利用します。
(底辺)²+(高さ)²=(斜辺)²
底辺をDH=2√2?
高さをOH=χ?
斜辺をOD=6?
(2√2)²+(χ)²=(6)²
8+χ²=36
χ²=36−8
χ²=28
χ=√28(χは+になります)
2)28
2)14
7
χ=2√7
OH=2√7?
正四角錘の体積は
(底面積)×(高さ)×1/3
(底面積)=4?×4?=16㎠
(高さ)=2√7?
(16)×(2√7)×1/3=32√7/3
答え 32√7/3㎤
(2)この立体の表面積を求めてください。

四角形ABCDの面積は
4×4=16㎠
△AOEを三平方の定理を利用して考えます。
(底辺)²+(高さ)²=(斜辺)²
底辺をAE=2cm
高さをOE=χ?
斜辺をOA=6?
(2)²+(χ)²=(6)²
4+χ²=36
χ²=36−4
χ²=32
χ=√32(χは+になります)
2)32
2)16
2) 8
2) 4
2
χ=4√2
OE=4√2?
△AODの面積は
底辺をAD=4?
高さをOE=4√2?
4×4√2×1/2=8√2
△AODの面積は8√2㎠
△OAD+△OAB+△OBC+△OCD=8√2×4=32√2㎠
四角ABCD=16㎠ですから、
(16+32√2)㎠
答え (16+32√2)㎠








コメント