中学1年数学 立体の表面積 練習問題1 解答・解説
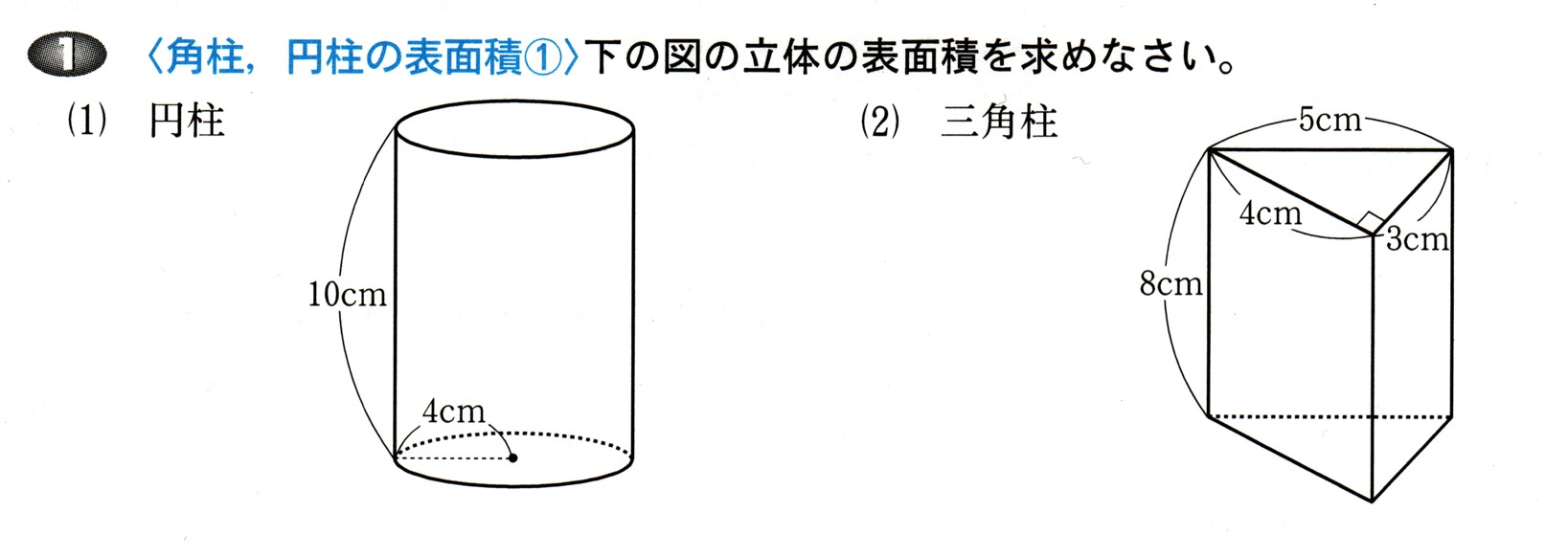
図の立体の表面積を求めてください。
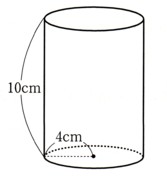
(1)
まずは、底面の面積を求めます。
底面の面積は、円ですから、円の面積の求め方は
円の面積=πγ²
(円の面積)=(半径)×(半径)×π
円の半径は、4cmですから
(円の面積)=4×4×π
=16π?²
次に、側面の面積を求めます
円柱の側面は、展開図にすると長方形になりますから
1辺×1辺、になります。
1つの辺の長さは、10cm
もう一辺は、円の円周の長さに等しくなります。
それでは、円の円周を求めましょう。
円の円周を求める式は、
(円周の長さ)=2πγ
(円周の長さ)=2×(半径)×π
円の半径は、4cmですから
(円周の長さ)=2×4×π
=8π?
これで、長方形の2つの辺の長さがわかりました。
10(?)×8π(?)=80π?²
になります
円柱の表面積は
(円柱の表面積)=(底面の面積)+(底面の面積)+(側面の面積)
=16π+16π+80π
=112π?²
答え 112π?²
(2)
まずは底面の面積を求めます。
底面は、直角三角形ですから、三角形の面積の求め方は
(三角形の面積)=(底辺)×(高さ)÷2
底辺を、3cmにすると
高さは、4cmになります。
=3×4÷2
=6?²
上の面(上底)と下の面(下底)は、同じ面積ですから。
6?²×2=12?² になります。
次に側面の面積を求めます。
側面の面積は、円柱と同じように、長方形になりますから
1辺×1辺になります
1辺の長さは 8cm で、もう1辺は直角三角形の周の長さになります。
三角形の周の長さは、底辺3cm+高さ4cm+斜辺5cmになります。
合計は、
(三角形の周の長さ)=(3cm)+(4cm)+(5cm)
=12?
これで、長方形の2つの辺の長さがわかりました
8cm×12?=96?²
三角柱の表面積は
(三角柱の表面積)=(上底面の面積)+(下底面の面積)+(側面の面積)
= 6?²+6?²+96?²
=108?²
答え 108?²


















コメント