中学３年数学　関数ｙ＝aχ²　まとめテスト5・解答

確認問題１（S+V+O+C)

中学理科1年　身のまわりの物質とその性質　物質の見分け方　確認問題２

中学1年数学　反比例・比例反比例の利用２　練習問題4　解答・解説

中学1年数学　直線図形と対称　基本の作図　確認問題4　解答・解説

中学2年数学　連立方程式　　まとめテスト８・解答

中学2年数学　連立方程式　いろいろな連立方程式　確認問題５･解答

中学2年数学　1次関数　１まとめテスト2・解答

中学2年数学　連立方程式　いろいろな連立方程式　練習問題３

中学3年数学　式の展開と因数分解　因数分解　練習問題７・解答（１）

中学2年数学　確率　２まとめテスト１・解答

中学２年数学　図形の調べ方　まとめテスト２・解答

中学2年数学　1次関数　2元1次方程式とグラフ　練習問題1・解答

中学2年数学　連立方程式　いろいろな連立方程式　　基本問題1・解答

練習問題2(文字を使った式2)

中学３年理科　生物の細胞と生殖　細胞と生物の成長　練習問題４・解答

中学2年数学　図形の調べ方　図形の合同　確認問題２

スポンサーリンク

中学1年数学　立方体の表面積　練習問題４　解答・解説

おうぎ形

2013.04.112009.09.29

中学1年数学　立方体の表面積　練習問題４　解答・解説

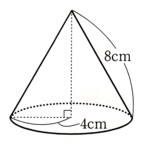
図のような、底面の半径が4cm、母線の長さが8cmの円錐について、次の問いに答えてください。

（１）側面の展開図のおうぎ形の中心角の大きさを求めてください。

おうぎ形の中心角の大きさを $\displaystyle x^\circ$ とすると。母線の長さが8cmですから、おうぎ形の半径も8cmということがわかります。

側面のおうぎ形の弧の長さは底面の円周の長さに等しくなりますから。

$\displaystyle2\pi\times8\times \frac{x}{360}$ = $\displaystyle2\pi\times4$

$\displaystyle\frac{16\pi x}{360}=8\pi$

両辺に $\displaystyle\frac{360}{8\pi}$ をかけます

$\displaystyle2x=360$

$\displaystyle x=180$

答え　180゜

（２）この円錐の側面積を求めてください。

側面積は、おうぎ形の面積となります。中心角を $\displaystyle x^\circ$ とすると、おうぎ形の面積は、

$\displaystyle \pi r^{2}\times\frac{x}{360}$

となります。

半径は、母線の長さになりますから8cmになります。

$\displaystyle =8\times8\times \pi \times \frac{x}{360}$

おうぎ形の中心角は（１）で求められているので、

$\displaystyle =8\times8\times \pi \times \frac{180}{360}$

$\displaystyle =64\pi\times\frac{1}{2}$

$\displaystyle =32\pi cm^{2}$

答え　32πcm²

（３）この円錐の表面積を求めてください。

　　　円錐の表面積は、1つの底面積と側面積の合計になります。

　　　　（円錐の表面積）＝（底面積）＋（側面積）

　　側面積は、おうぎ形の面積になりますから、

　　　おうぎ形の面積は（２）で32?²と、わかりましたから
　　　　　　　　　　　　
　　　　　（円錐の表面積）＝（底面積）＋（32?²）

　　　底面積は、半径4cmの円の面積になります。

　　円の面積の求め方は

　　　　(円の面積)＝πγ²

　　　　　　　　　＝半径×半径×π

　　半径は4cmになりますから

　　　　　　　　　＝4×4×π

　　　　　　　　　＝16π?²

　　　　　（円錐の表面積）＝（16π?²）＋（32π?²）

　　　　　　　　　　　　　＝48π?²

　　　　答え　　48π?²

コメント