中学2年数学 式の計算 式の利用 2練習問題3・解答
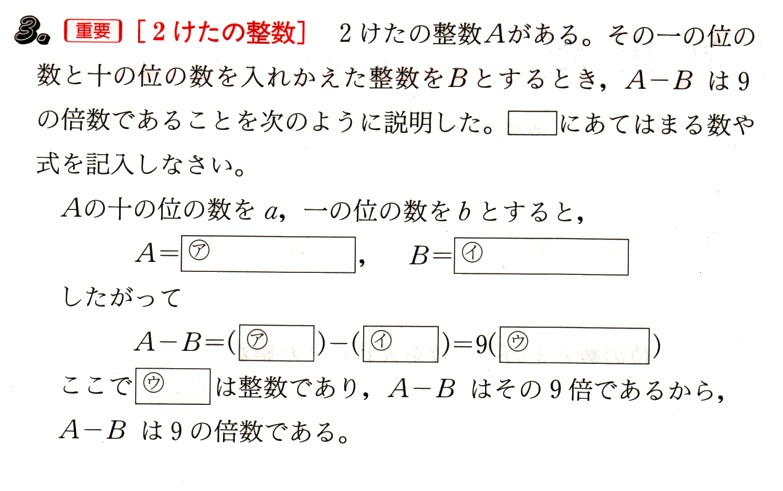
3,2桁の整数
2桁の整数Aがあります。その一の位の数と十の位の数を入れ替えた整数をBとするとき、A–Bは9の倍数であることを次のように説明しました。[ ]にあてはまる数や式を記入してください。
A=ア[ ],B=イ[ ]
したがって
A−B=(ア[ ])−(イ[ ])=9(ウ[ ])
ここでウ[ ]は整数であり、A−Bはその9倍であるから、
A−Bは9の倍数である。
2桁の整数Aがあります。その一の位の数と十の位の数を入れ替えた整数をBとするとき、A-Bは9の倍数であることを次のように説明しました。[ ]にあてはまる数や式を記入してください。
A=ア[10a+b ],B=イ[10b+a ]
したがって
A−B=(ア[10a+b])−(イ[10b+a])=9(ウ[ a−b ])
ここでウ[ a−b ]は整数であり、A−Bはその9倍であるから、
A−Bは9の倍数である。
Aの十の位の数をa、一の位の数をbとすると、
A=10a+b、B=10b+a となりますから、A−Bを計算すると、
(10a+b)−(10b+a)=9(a−b)
になります。
9の倍数ということがわかります。










コメント