中学2年数学 式と計算 2まとめテスト2・解答
2,A=χ/2 −y+3z、B=4χ −y/3+z、C=−2χ+y+ 2/3z とするとき、A/3 − B+C/2 を、χ、y、zの式で表してください。
A/3 − B+C/2 に A=χ/2 −y+3z、B=4χ −y/3+z、C=−2χ+y+ 2/3z を代入していきます。
(χ/2 −y+3z)/3 − (4χ −y/3+z)+(−2χ+y+ 2z/3)/2
分母をそろえます。
=2(χ/2 −y+3z)−3{(4χ −y/3+z)+(−2χ+y+2z/3)}/6
=2(χ/2 −y+3z)−3{4χ −y/3+z−2χ+y+2z/3}/6
=2(χ/2 −y+3z)−3{4χ−2χ −y/3+3y/3+2z/3+z}/6
=2(χ/2 −y+3z)−3(2χ+2y/3+5z/3)/6
=χ−2y+6z−6χ−2y−5z/6
同類項をまとめます。
=χ−6χ−2y−2y+6z−5z/6
=−5χ−4y+z /6
=−5χ/6−2y/3+z/6
答え −5/6 χ−2/3 y+1/6 z,
=6(−5χ/6−2y/3+z/6)
=−5χ−4y+z











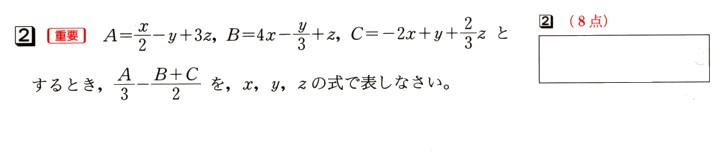

コメント