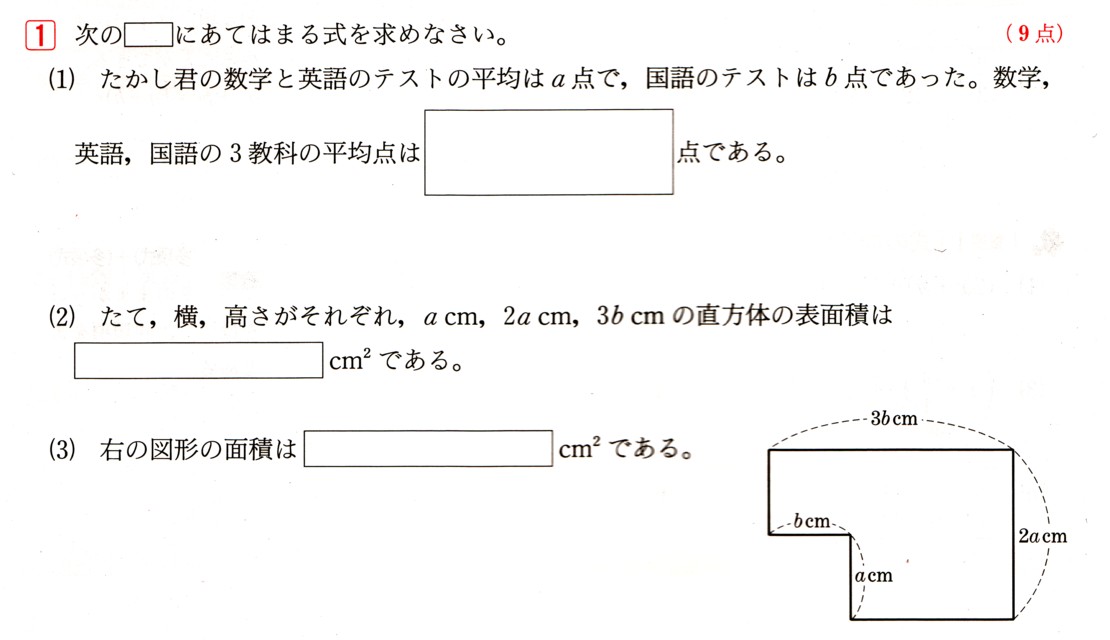
1、次の[ ]にあてはまる式を求めてください。
(1)たかし君の数学と英語のテストの平均点はa点で、国語のテストはb点でした。数学、英語、国語の3教科の平均点は[ ]点でした。
2つの平均点は、n+m÷2、
3つの平均点は、n+m+l+÷3
になります。
今回は、数学と英語の平均点は、a点になりますから、式にすると
(数学)+(英語)÷2=a(点)[1教科の平均の点数]
例:数学80(点)、英語60(点)、国語70(点)とします。
数学+英語=80+60=140
平均点は、140÷2=70点[1教科の平均の点数]になります。
数学と英語の平均点に国語の点数を加えて、3教科の平均を出してみます。
〔数学と英語の平均点〕70(点)+70(点)+〔国語の点数〕70(点)÷3=210÷3=〔3教科の平均〕70(点)
確かめてみましょう。
数学+英語+国語=80+60+70=210
平均点は、210÷3=70
(数学)+(英語)の平均点はa(点)で2教科ですから。
a+a=2a
になります。
これに〔国語の点数〕b(点)を加えると
2a+b÷3
この式を簡単にすると
2a+b/3
となります。
答え 2a+b/3
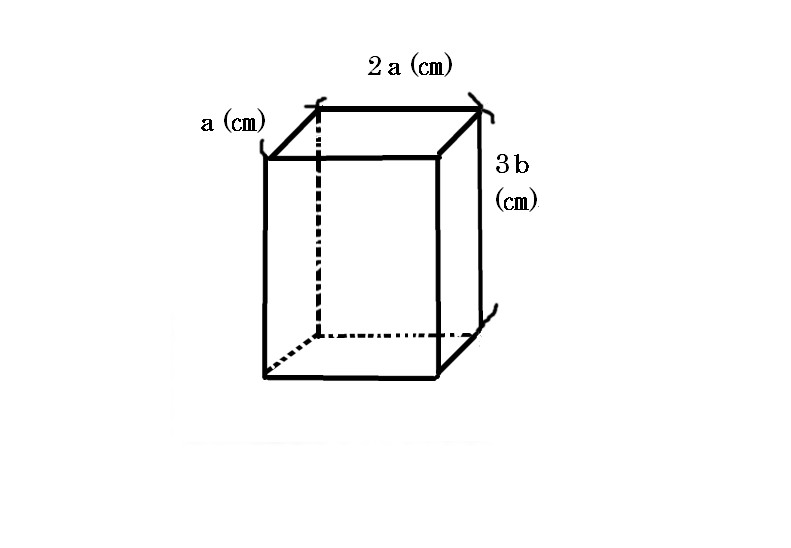
(2)縦、横、高さがそれぞれ、a(?)、2a(?)、3b(?)の直方体の表面積は[ ]㎠になります。
まずは、図 を考えていきます。それを展開図にするとこのような図
を考えていきます。それを展開図にするとこのような図 になります。
になります。
いくつかの考え方はありますが、今回は、3色の長方形で考えていきましょう。
青い長方形・・・2a×3b
赤い長方形・・・a×3b
黄色い長方形・・・2a×a
それぞれの色の長方形の数は2個ずつありますから
2×(〔青い長方形〕+〔赤い長方形〕+〔黄色い長方形〕)=〔直方体の表面積〕
2(2a×3b+a×3b+2a×a)
=2(6ab+3ab+2a²)
=2(9ab+2a²)
=18ab+4a²
答え 18ab+4a²(㎠)
まずは、黄色い図形と赤い図形を足した長方形の面積を求め。その図形から赤い図形の面積 を引けば黄色い図形の面積がわかります。
を引けば黄色い図形の面積がわかります。
全体の面積は、 3b×2a=6ab(㎠)
赤い図形の面積は、a×b=ab(㎠)
〔全体の面積〕−〔赤い図形の面積〕=〔黄色い図形の面積〕
↓ ↓
6ab − ab =5ab(㎠)
答え 5ab(㎠)







コメント