中学２年数学　１次関数　2元１次方程式とグラフ　確認問題４・解答

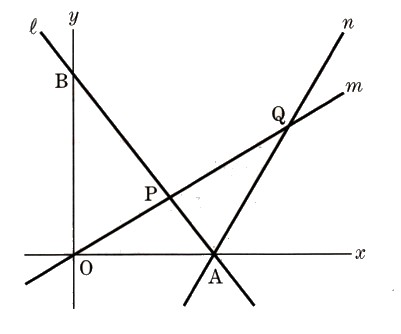
４、次の図で、直線ℓは方程式　4χ+3ｙ＝12　のグラフでχ軸、ｙ軸とそれぞれ点Ａ，Ｂで交わります。

　　直線ｍは関数　ｙ＝ａχ(ａ＞0)のぐらふで、直線ℓと点Ｐで交わります。

　　また、直線ｍ上に、ｙ座標が正の点Ｑがあり、2点Ａ，Ｑを通る直線ｎとします。このとき、次の問いに答えてください。

（１）点Ｂの座標を求めてください。

　　点Ｂの座標は、(χ、ｙ)＝(0、ｙ)　ということになります。

　　点Ｂに接している直線は直線ℓですから、直線ℓの方程式を ｙ＝ａχ＋ｂ　の形にします。

　　4χ＋3ｙ＝12

　　3ｙ＝−4χ＋12

　　ｙ＝−4/3 χ ＋4

　　ｙ＝(傾き)χ＋(切片)

　　(切片)は、ｙ軸に接する座標になりますから、＋４ということになります

　(χ、ｙ)＝（0、4）になります。

　　答え　(χ、ｙ)＝（0、4）

（２）線分ＯＡの中点をとおり、直線ℓに平行な直線の式を求めてください。

　　　　まずは、線分ＯＡの中点を求めます。

　　　線分ＯＡの中点は、直線ℓがχ軸に接する座標ということがわかります。

　　そのχ軸に接する座標と原点Ｏと線分ＯＡの中間が中点ということがわかります。

　　直線ℓの式は、ｙ＝−4/3 χ ＋4　

　　　だということはわかっていますから、

　　その式に　(χ、ｙ)＝(χ、0)　を代入します。

　　(0)＝−4/3 χ ＋4

　　　0＝−4/3 χ ＋4

　　　−4/3 χ ＋4＝0

　　　−4/3 χ＝−4

　　　χ＝−4×（−3/4）　

　　　χ＝3

　　　直線ℓがχ軸に接する座標が(3，0)ということがわかりました。
　　　
　　　原点から中点までが３ということがわかりましたから、その半分が中点になります。

　　　3÷2＝1.5

　　次に、直線ℓに平行な直線について考えます。

　　平行な直線は、傾きが同じですから、直線ℓの傾きを見てみます。

　　ｙ＝−4/3 χ ＋4

　　ｙ＝(傾き)χ＋(切片)

　　傾きが　−4/3 　ということがわかりました。

　　ということは、

　　　ｙ＝−4/3 χ ＋ｂ

　　を求めるために、ｙ＝−4/3 χ ＋ｂ　の式に、(1.5，0)を代入します。

　　（0）＝−4/3 (1.5)＋ｂ

　　（0）＝−4/3 (3/2)＋ｂ

　　0＝−2＋ｂ

　　−2＋ｂ＝0

　　　ｂ＝2

　　(切片)が2ということがわかりました。

　　ｙ＝(傾き)χ＋(切片)

　　(傾き)＝−4/3

　　(切片)＝2

　　　ｙ＝ａχ＋ｂ

　　ｙ＝−4/3χ＋2

　　直線ℓに平行な線分ＯＡの中点を通る直線の式がわかりました。

　　　答え　ｙ＝−4/3χ＋2

（３）ａ＝2/3　のとき、三角形ＡＰＱと三角形ＯＢＰの面積が等しくなるような直線ｎの式を求めてください。

　　△ＡＰＱ＝△ＯＢＰが等しくなる三角形は、△ＡＯＢ＝△ＡＯＱが等しいといえます。

　　三角形の面積は(底辺)×（高さ）÷2

　　底辺をＯＡとすると、高さも同じということになります。図

　　△ＡＯＢの(底辺)は　3　、(高さ)は直線ℓの切片＝4　とわかっていますから

　　△ＡＯＱの(底辺)の長さは△ＡＯＢと共通ですから　3

　　(高さ)は、(面積)が同じなのですから　4　となります。

　　これで、直線ｎの点Ｑのｙ＝4　がわかりました。

　　点Ｑは、直線ｍの座標でもありますから、直線ｍの式にｙ＝4を代入してχの座標をみつけます。

　　直線ｍは、　ｙ＝ａχ　で、ａ＝2/3　ですから

　　　ｙ＝2/3χ　になり、この式に　ｙ＝4　を代入します。

　　　4＝2/3χ

　　　2/3χ＝4

　　　χ＝4×3/2

　　　χ＝6

　　　直線ｍのχの座標がχ＝6と、わかりました

　　　この。直線ｍのχ座標は、直線ｎのＱ点のχ座標にもなります。

　　　ｙ座標は、すでにｙ＝4とわかっているので、

　　　直線ｍのＱ点は（χ、ｙ）＝（6、4）になります。

　　これで、連立方程式を使って点Ｑ（6、4）、点Ａ（3、0）を通る直線ｎの式を求めます。

　　ｙ＝ａχ＋ｂ　の式に(χ、ｙ)を代入していきます。

　　（4）＝ａ（6）＋ｂ
　｛
　　（0）＝ａ（3）＋ｂ

　　
　　　6a＋ｂ＝4
　｛
　　　3ａ＋b＝0

　　　6a＋ｂ＝4
　−)3ａ＋b＝0
　　　3ａ　＝4

　ａ＝4/3

　　6a＋ｂ＝4　に　ａ＝4/3　を代入します。

　　6（4/3）＋ｂ＝4

　　8＋ｂ＝4

　　ｂ＝4−8

　　ｂ＝−4

　　　これで、直線ｎの式がわかりました。

　　　答え　ｙ＝4/3χ−4