中学2年数学　1次関数　1次関数の応用　確認問題5・解答

中学2年数学　1次関数　1次関数の応用　確認問題5・解答

５、図のように、

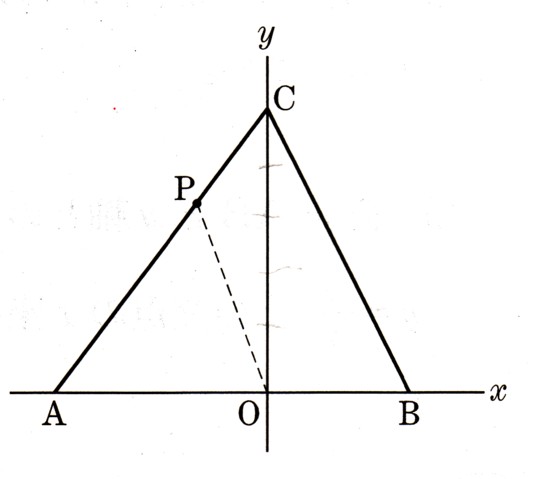
　A（−３，０）
　B（２，０）
　C（０，４）

　　を頂点とする△ＡＢＣの辺ＡＣ上に点Ｐを取ります。直線ＯＰが△ＡＢＣの面積を2等分するとき、点Ｐの座標を求めて下さい。

　
　　△ＡＢＣの面積の半分にが通ればいいのですから、△ＡＢＣの面積÷２の位置になります。

　　△ＡＢＣの面積は、底辺が、３＋２＝５

　　　　　　　　　　      　高さが、４

　　　５×４÷２＝１０平方

　　　とわかります。

　　　△ＡＢＣの面積はその半分ですから、

　　　１０÷２＝５(平方)

　　　になります。　　　

　　　△ＡＢＣの面積が５になる座標Ｐの位置を考えます。

　　　△ＡＢＣの底辺は、辺ＡＯになりますから

　　　底辺＝３になります。

　　　高さを求めれば、Ｐ点の座標がわかります。

　　　高さは、ｙ軸になりますから

　　　(面積)＝(底辺)×(高さ)÷２

　　　　５　＝　３　×　ｙ　÷２

　　　　５＝３/２ｙ

　　　　　ｙ＝５×２/３

　　　　　ｙ＝１０/３

　　　このｙの座標を辺ＡＣの式に代入すれば点Ｐのχ座標がわかります。

　　ｙ＝ａχ+ｂ　にしてみます。

　　　　　　   (ｙの増加量)　　   4
　　(傾き)＝――――――＝――　　
　　　　　  　(χの増加量)　　  3

　　　になります。

　　(切片)はｙ軸に接する点ですから、（０．４）ですから、

　　　４　になります。

　　　ｙ＝4/3 χ　＋４　になりますから、この式に、ｙ＝１０/３　を代入します。

　　　10/3＝4/3 χ　＋４

　　　4/3 χ　＋４＝10/3

　　　4/3χ＝10/3−12/3

　　　4/3χ＝−2/3

　　　χ＝−2/3×3/4

　　　χ＝−6/12

　　　χ＝-1/2

　　　　これで、点Ｐが△ＡＢＣを2等分する線分ＯＰのＰ座標がわかりました。

　　　　答え　(χ、ｙ)＝(−1/2、10/3)