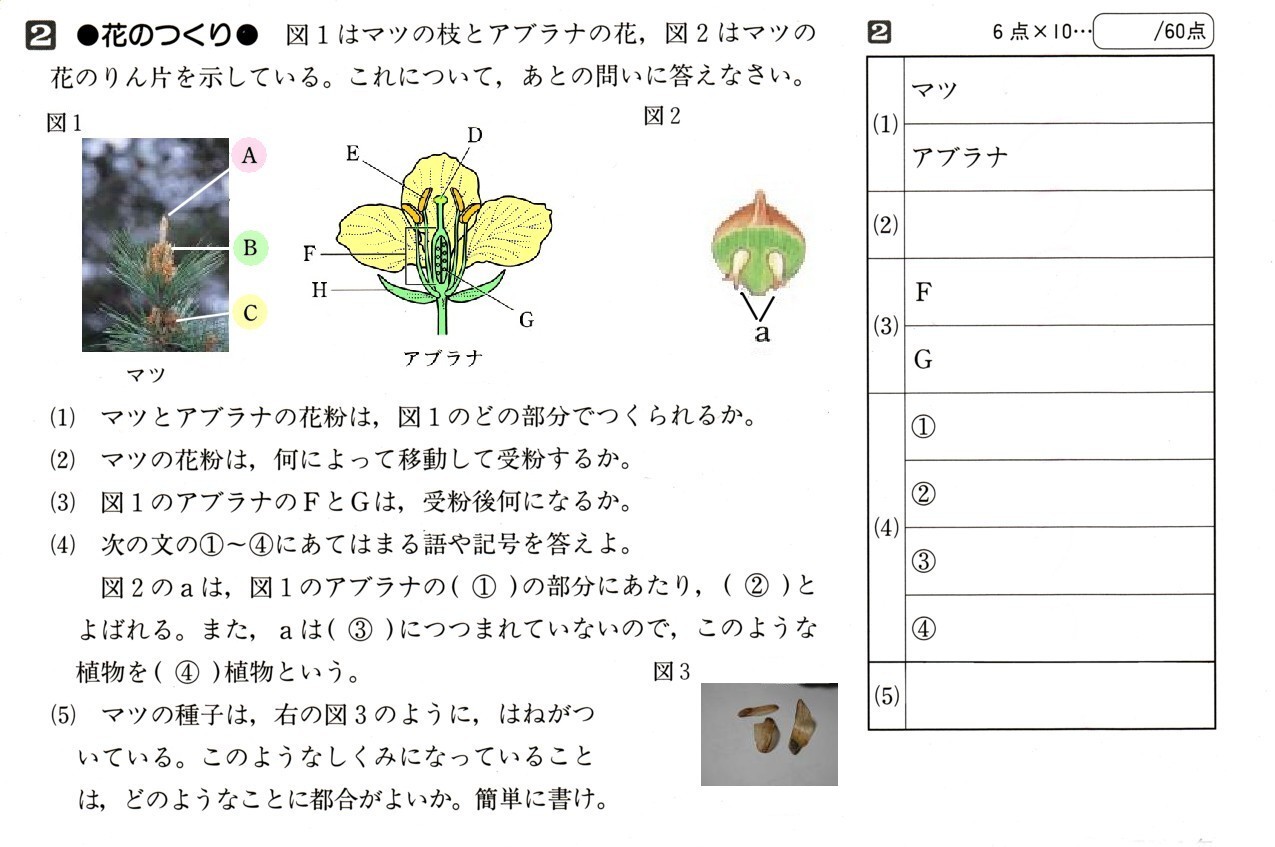
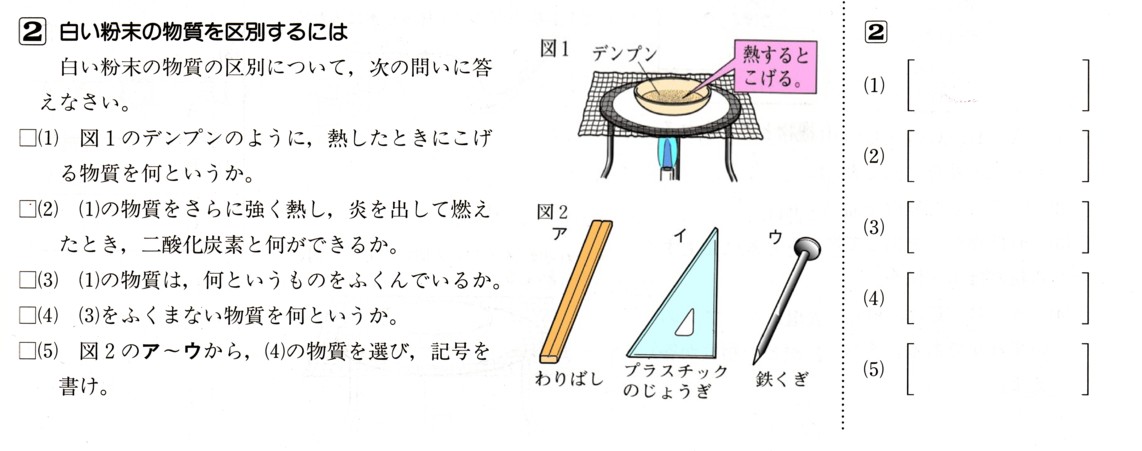
中学2年数学 1次関数 1まとめテスト3・解答
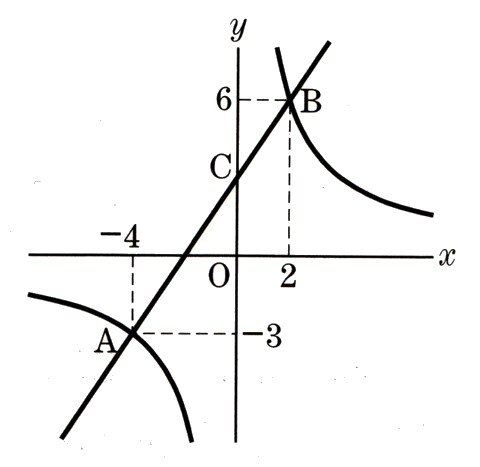
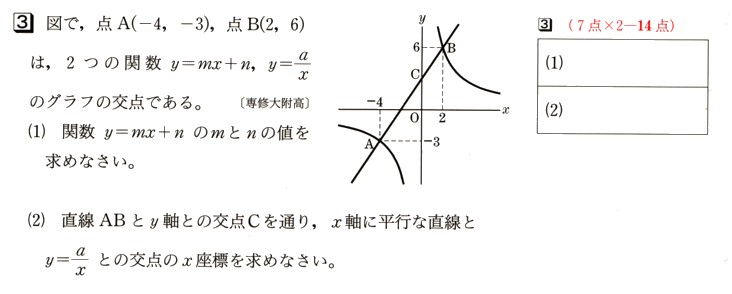
3、図 で、点A(−4、−3)、点B(2,6)は、2つの関数 y=mχ+n 、y=a/χ のグラフの交点になります。
で、点A(−4、−3)、点B(2,6)は、2つの関数 y=mχ+n 、y=a/χ のグラフの交点になります。
(1)関数 y=mχ+n のmとnの値を求めて下さい。
図 を見てみると、2つの線があります。1つは、直線でもう1つは曲線になります。
を見てみると、2つの線があります。1つは、直線でもう1つは曲線になります。
直線は、比例の式になりますから、y=aχ+b の式となります。
m(傾き)、n(切片) になります。
この式の、m、nの解を求めるためには、2つの座標がわかっていますから、2元1次式で求めます。
連立方程式をつくり、点A(−4、−3)、点B(2,6)座標を代入します。
−3=−4m+n
{
6= 2m+n
−4m+n=−3
{
2m+n=6
−4m+n=−3
−) 2m+n=6
−6m =−9
m=3/2
6= 2m+n に m=3/2 を代入します。
6= 2(3/2)+n
2(3/2)+n=6
3+n=6
n=6−3
n=3
答え m=3/2 、n=3
(2)直線ABとy軸との交点Cを通り、χ軸に平行な直線と y=a/χ との交点のχ座標を求めて下さい。
直線ABの式は(1)から
y=3/2χ+3
y軸に接する直線ABは、y=3/2χ+3 の式の(切片)になりますから、
y=3/2χ+3 の式のy軸が 3 とわかります。
つぎに、 y=a/χ の式に点A(−4、−3)、点B(2,6)を代入して、連立方程式をつくります。
−3=a/−4
{
6=a/2
a/−4=−3
{
a/2=6
a=−3×−4
{
a=6×2
a=12
{
a=12
a=12 がわかりました。
y=12/χ となります。
この式 y=12/χ にy=3/2χ+3 の式のy軸が 3 を代入します。
3=12/χ
3χ=12
χ=4
χ軸に平行な直線とy=12/χ の式の交点の座標がわかりました
(χ、y)=(4,3)
たずねているのは、χになります。
答え 4










コメント