中学2年数学 図形の調べ方 図形の合同 確認問題2・解答
2、正三角形ABCの辺BC、CA上にBP=CQとなるように2点P、Qをとり、AとP、BとQを結ぶとき、△ABP≡△BCQとなることを証明してください。
答え 

△ABPと△BCQにおいて
仮定よりAB=BC・・・?
BP=CQ・・・?
△ABCは正三角形ですから
∠ABP=60°
∠BCQ=60°
∠ABP=∠BCQ・・・?
?〜?より
2辺とその間の角がそれぞれ等しくなるので、
△ABP≡△BCQ
 数学
数学  大地
大地  因数分解
因数分解  水溶液
水溶液  地震
地震  数学
数学  レンズ
レンズ  数学
数学  数学
数学  平面図形
平面図形  数学
数学  数学
数学 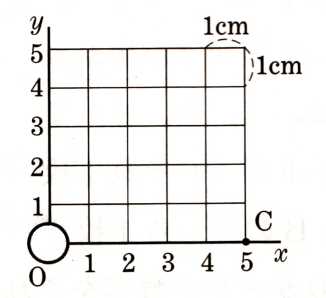 数学
数学 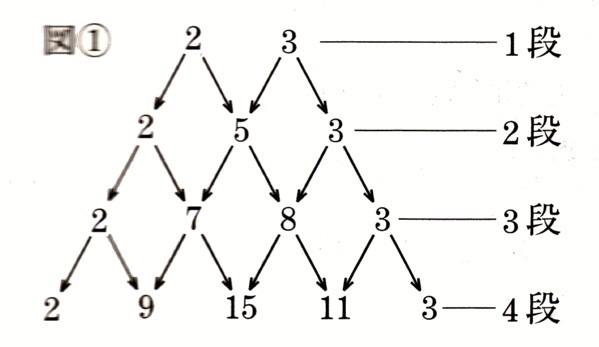 数学
数学  数学
数学  平方根
平方根 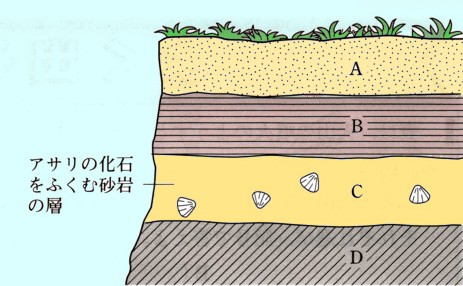 化石
化石 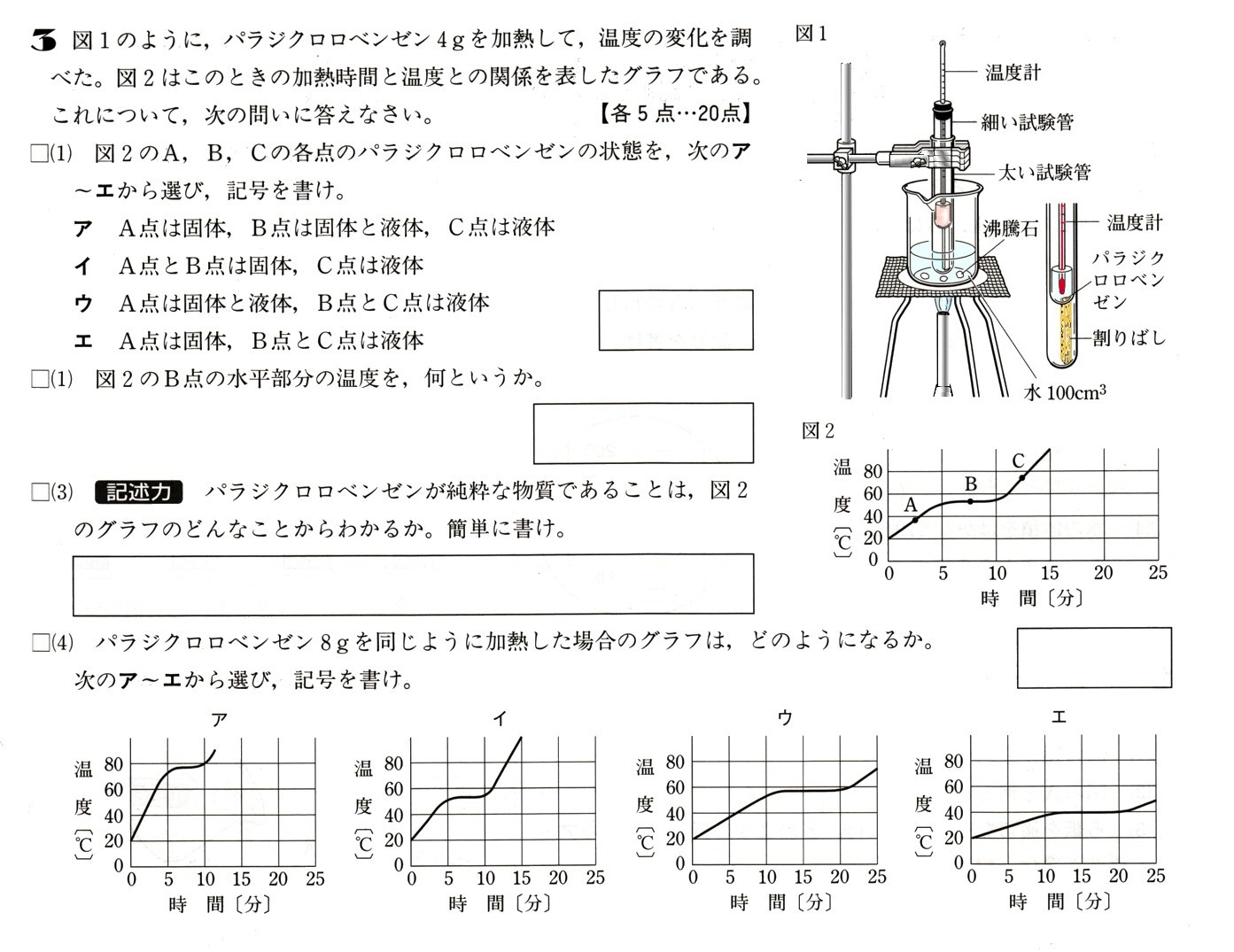 水溶液
水溶液 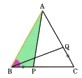 合同
合同中学2年数学 図形の調べ方 図形の合同 確認問題2・解答
2、正三角形ABCの辺BC、CA上にBP=CQとなるように2点P、Qをとり、AとP、BとQを結ぶとき、△ABP≡△BCQとなることを証明してください。
答え 

△ABPと△BCQにおいて
仮定よりAB=BC・・・?
BP=CQ・・・?
△ABCは正三角形ですから
∠ABP=60°
∠BCQ=60°
∠ABP=∠BCQ・・・?
?〜?より
2辺とその間の角がそれぞれ等しくなるので、
△ABP≡△BCQ
コメント