中学3年数学 関数y=aχ²の値の変化 2確認問題3・解答
3、関数y=aχ²(a>0)のグラフ上に3点A,B,Cがあります。それらの点のχ座標はそれぞれ−2,1,3になります。このとき、次の問いに答えてください。
(1)a=2のとき、2点A,Cを通る直線の式を求めてください。
まずは、それぞれのχ座標 (−2,1,3)はどの点の座標なのかを考えます。
A,B,Cの中でχ座標が負になるのは点Aですから点A座標(−2、?)
次に、χ座標が一番大きな数になるのは点Cですから点C座標(3、?)
残った1が点B座標のχになります。点B座標(1、?)
まずはy=aχ²の式にあてはめて考えます。
a=2ですから、y=2χ²で考えます。
(点Aの座標)=(−2、y)、(点Cの座標)=(3、y)
y=2×(−2)² y=2×3²
y=2×4 y=2×9
y=8 y=18
(点Aの座標)=(−2、8)、(点Cの座標)=(3、18)
点A,点Cのそれぞれの座標がわかりましたから、
直線ACの式(y=aχ+b)にあてはめます。
8=−2a+b 18=3a+b
8=−2a+b
−)18=3a+b
−10=−5a
a=2
18=3a+bにa=2を代入します。
18=3×2+b
18=6+b
b=18−6
b=12
傾きが2で切片が12ということがわかります。
答え y=2χ+12

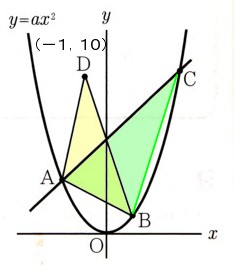
(2)点Dの座標が(−1.10)のとき、△ABCと△ABDの面積が等しくなるように、aの値を求めてください。
△ABCと△ABDが等しくなるには、底辺になる辺ABに平行な線DCにならなければいけません!
平行な直線DCは直線ABと傾きが同じになります、傾きは変化の割合になりますから、
yの増加量
変化の割合=――――――
χの増加量
になります。
y=aχ² の式に分かっているχ座標を代入しy座標を求めます。
点Aは(−2、y) y=a×(−2)²=4a (−2、4a)
点Bは(1、y) y=a×1=a (1、a)
点Cは(3、y) y=a×3²=9a (3、9a)
点Dは(−1,10)

直線ABの変化の割合=直線DCの変化の割合
a−4a 9a−10
――――=――――
1−(−2) 3−(−1)
−3a 9a−10
―――=――――
3 4
−12a 27a−30
――― =――――
12 12
−12a=27a−30
−12a−27a=−30
−39a=−30
a=30/39
a=10/13
になります。
答え a=10/13






コメント