中学3年数学 図形と相似 まとめテスト5・解答
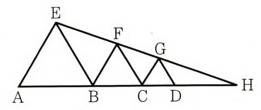
5、次の図 で、4点A,B,C,Dは一直線上にあり、△ABE,△BCF、△CDGは、
で、4点A,B,C,Dは一直線上にあり、△ABE,△BCF、△CDGは、
それぞれAB,BC,CDを1辺とする正三角形になります。
3点E,F,Gは一直線上にあり、HはADの延長とEGの延長との交点になります。
AE=6cm、AH=18cmのとき、次の問いに答えてください。
(1)線分BFの長さを求めてください。
△HAE と△HBFで考えます。
 △AEBは正三角形ですから、ABの長さも6?になります。
△AEBは正三角形ですから、ABの長さも6?になります。
これにより、BHの長さは、AHからABの長さを引けばわかります。
AH=18?
AB =6?
BH =18−6=12?
△HAE∽△HBF ですから、
AH :AE=BH:BF になります。
ですから、
18 :6=12:BF
18 ×BF=6×12
18 BF=72
BF =72/18=4
答え BF=4?
(2)線分DHの長さを求めてください。

(1)でBF=4?とわかりましたから、
△BFC は正三角形ですから
BC=4?
CH =AH−(AB+BC)
AH=18?
AB=6?
BC=4?
CH =18−(6+4)
CH=8?
△HCGと△HBFで
△HCG∽△HBF ですから
HC:HB=CG:BF
HC=8?
HB=4?+8?=12?
BF=4?
8:12=CG:4
8×4=12×CG
12CG=32
CG=32/12=16/6=8/3
これにより、△CGDは正三角形ですから、
CDの長さも8/3?になります。
これにより、DHの長さは
AH−(AB+BC
+CD)=DH
AH=18?
AB=6?
BC=4cm
CD=8/3cm
18−(6+4+8/3)=DH
18−(30/3+8/3)=18−38/3
=54/3−38/3
=16/3
答え 16/3cm






コメント