中学2年数学 平面図形 平行線と面積 確認問題6・解答
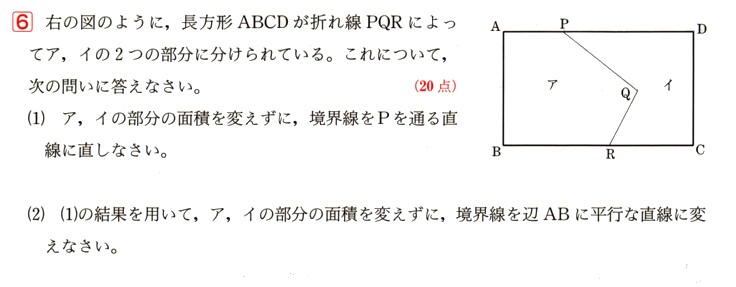
6、図のように、長方形ABCDが折れ線PQRによってア、イの2つの部分に分けられています。これについて次の問いに答えてください。
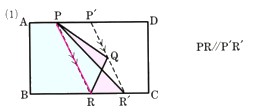
(1)ア、イの部分の面積を変えずに、境界線をPを通る直線に直してください。
PRに平行な点Qを通る直線をかき、BCに交わる点をR’とします。
点Pと点R’とをつなぐ直線をかきます。
この台形ABR’Pと五角形ABRQPは同じ面積になります。
答え 

(2)(1)の結果を用いて、ア、イの部分の面積を変えずに、境界線を辺ABに平行な直線に変えてください。
(1)でできた台形ABR’Pの辺PR’の中点をかきます、この中点をMとします。
辺ABに平行な点Mを通る線をかきます。
辺ADに交わる点をYとし、辺BCに交わる点をXとします。
YとXを結ぶ線をかきます。
できた、四角形ABXYは、台形ABR’Pと同じ面積で辺ABに平行な図形になります。
答え 









コメント