中学２年数学 図形の調べ方 図形と証明 確認問題7・解答
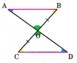
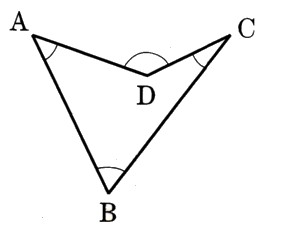
７、図
で、∠ＡＤＣ＝∠Ａ＋∠Ｂ＋∠Ｃが成り立つことについて、次の問いに答えてください。
で、∠ＡＤＣ＝∠Ａ＋∠Ｂ＋∠Ｃが成り立つことについて、次の問いに答えてください。（１）花子さんは次のように証明しました。㋐、㋑にあてはまる言葉を、㋒にあてはまる角を書き入れて、証明を完成させてください。
〔証明〕
点Ｄを通る直線ＢＥを引く。三角形の（ｱ ）は、それと隣り合わない（ｲ ）の和に等しいから、
（ｳ ）＝∠Ａ＋∠ＡＢＤ，∠ＣＤＥ＝∠ＣＢＤ＋∠Ｃ
よって、（ｳ ）＋∠ＣＤＥ＝∠Ａ＋∠ＡＢＤ＋∠ＣＢＤ＋∠Ｃ
ゆえに、∠ＡＤＣ＝∠Ａ＋∠Ｂ＋∠Ｃ
〔証明〕
点Ｄを通る直線ＢＥを引く。三角形の（ｱ 外角 ）は、それと隣り合わない（ｲ ２つの内角 ）の和に等しいから、
（ｳ ∠ＡＤＥ ）＝∠Ａ＋∠ＡＢＤ，∠ＣＤＥ＝∠ＣＢＤ＋∠Ｃ
よって、（ｳ ∠ＡＤＥ ）＋∠ＣＤＥ＝∠Ａ＋∠ＡＢＤ＋∠ＣＢＤ＋∠Ｃ
ゆえに、∠ＡＤＣ＝∠Ａ＋∠Ｂ＋∠Ｃ
答え ア、 外角 イ、 ２つの内角 ウ、∠ＡＤＥ
（２）花子さんとは別の方法で証明してください。ただし、証明に必要な補助線や点は図に書き入れてください。
答え 
〔証明］
ＣＤの延長線を引きその点をＦとし、ＡＢの交点をＥとします。
外角は、それと隣り合わない２つの内角の和に等しくなりますから、
∠ＤＣＢ＋∠ＥＢＣ＝∠ＦＥＢ
対頂角により
∠ＦＥＢ＝∠ＡＥＤ
外角は、それと隣り合わない２つの内角の和に等しくなりますから、
∠ＡＤＣ＝∠ＡＥＤ＋∠ＤＡＥ
直線は、180°ですから、
∠ＡＤＥ＋∠ＡＤＣ＝180°
よって、
∠ＡＤＣ＝∠Ａ＋∠Ｂ＋∠Ｃ
になります。
コメント