中学3年数学 三平方の定理の利用 2確認問題2・解答
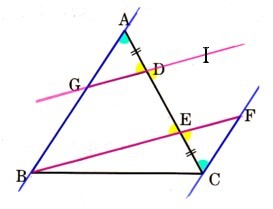
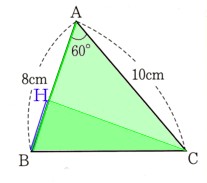
2、図 の△ABCにおいて、次の問いに答えてください。
の△ABCにおいて、次の問いに答えてください。
(1)ABを底辺としたときの高さを求めてください。
点Cから辺ABに垂線を引きます。
辺ABをの交点をHとして考えます。
そうすると、高さはCHの長さになります。
次に△AHCで考えます。
△AHCは直角三角形になりますから、
辺の長さに比は(底辺):(斜辺):(高さ)=1:2:√3
△AHCの底辺をAH,高さをCH,斜辺をAC
とします。
高さCHをχとして考えます。
(斜辺):(高さ)=2:√3=10:χ
2×χ=10×√3
2χ=10√3
χ=5√3
χ=CH=5√3?
答え 5√3?
(2)BCの長さを求めてください。

△AHCを三平方の定理で考えます。
辺の長さに比は(底辺):(斜辺):(高さ)=1:2:√3
底辺の長さをχとして考えます。
斜辺が10cmですから、
(底辺):(斜辺)=1:2=χ:10
1×10=2×χ
10=2χ
χ=5
底辺は5?になります。
AH=5
AB=8cmですから
BHの長さは、
BH=AB−AH
BH=8−5
BH=3
次に△BHCを三平方の定理を使い考えます。
底辺をHB=3cm
高さをCH=5√3?
斜辺をCB=χ?
として考えます。
(底辺)²+(高さ)²=(斜辺)²
3²+(5√3)²=χ²
9+25×3=χ²
9+75=χ²
84=χ²
χ=√84(χは+になります。)
2)84
2)42
21
χ=2√21
χ=BC=2√21
答え 2√21?










コメント