中学2年　1次関数　1次関数のグラフと式の求め方 練習問題1・解答

中学2年　1次関数　1次関数のグラフと式の求め方  練習問題1・解答

１、1次関数のグラフ

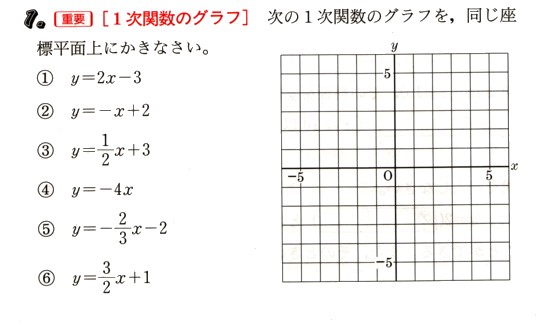
　　　次の1次関数のグラフを、同じ座標平面上に書いてください。

　?　ｙ＝2χ−3

　?　ｙ＝−χ＋2

　?　ｙ＝1/2 χ＋3

　?  ｙ＝-4χ

　?　ｙ＝-2/3 χ−2

　?　ｙ＝3/2 χ＋1
　

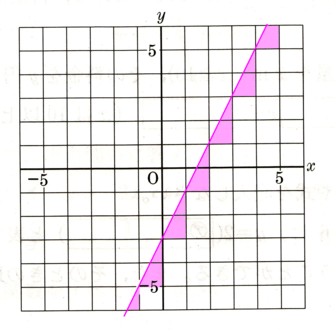
  直線の傾きは

　〔1〕ｙ＝ａχ＋ｂ　のグラフは、右ａ＞0のときは上がりになり、

　　　　　　　　　　　　　　　　　ａ＜0のときは右下がりになります。

　　　　ｙ＝(傾き)χ＋(切片)

　　　　　になります。

　?　ｙ＝2χ−3

　　　　ｙ＝(傾き)χ＋(切片)

　　　　ですから、

　　　　(傾き)が、2　となり

　　　　(切片)が、−3　となります。

　　　　（傾き）＝（ａ）

　　　　ａ＝2　で　ａ＞0　ですから

　　　　右上がりの直線になります。

 　　　　　答え　　

　?　ｙ＝−χ＋2

　　　　ｙ＝(傾き)χ＋(切片)

　　　　ですから、

　　　　(傾き)が、−1　となり

　　　　(切片)が、2　となります。

　　　　（傾き）＝（ａ）

　　　　ａ＝−1　で　ａ＜0　ですから

　　　　右下がりの直線になります。

      　　　答え　　

　?　ｙ＝1/2 χ＋3

　　　　ｙ＝(傾き)χ＋(切片)

　　　　ですから、

　　　　(傾き)が、1/2　となり

　　　　(切片)が、3　となります。

　　　　（傾き）＝（ａ）

　　　　ａ＝1/2　で　ａ＜0　ですから

　　　　右上がりの直線になります。

        　　　答え　　

　?  ｙ＝-4χ

　　　　ｙ＝(傾き)χ＋(切片)

　　　　ですから、

　　　　(傾き)が、-4　となり

　　　　(切片)が、0　となります。

　　　　（傾き）＝（ａ）

　　　　ａ＝-4　で　ａ＜0　ですから

　　　　右下がりの直線になります。

      　　　答え  

　?　ｙ＝-2/3 χ−2

　　　　ｙ＝(傾き)χ＋(切片)

　　　　ですから、

　　　　(傾き)が、-2/3　となり

　　　　(切片)が、−2　となります。

　　　　（傾き）＝（ａ）

　　　　ａ＝-2/3　で　ａ＜0　ですから

　　　　右下がりの直線になります。

       　　　答え   

　?　ｙ＝3/2 χ＋1

　　　　ｙ＝(傾き)χ＋(切片)

　　　　ですから、

　　　　(傾き)が、3/2　となり

　　　　(切片)が、1　となります。

　　　　（傾き）＝（ａ）

　　　　ａ＝3/2　で　ａ＞0　ですから

　　　　右上がりの直線になります。

 　　　答え