中学2年数学　1次関数　2元1次方程式とグラフ　練習問題6・解答

中学2年数学　1次関数　2元1次方程式とグラフ　練習問題6・解答

６、直線の交点（２）

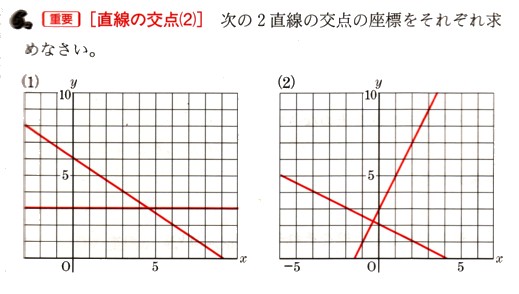
　　次の2直線の交点の座標をそれぞれ求めてください。

　　それぞれの直線の方程式を求め、連立方程式をつくり解くことで2直線の交点の座標がわかります。

（１）

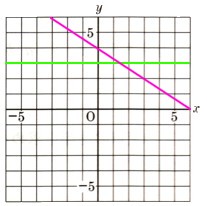
　　まずは、平行な直線は、χ軸に対して平行ですから、χ＝0になり、

　y＝3　になります。

　　つぎに、右下がりの直線について考えます。

　　y＝aχ＋b

　　y＝（傾き）χ＋（切片）

　　　　　    （ｙの増加量）
　　傾き＝―――――――＝ａ
　　　　   　（χの増加量）

　　右下がりの直線ですから、（傾き）の符号は（−）になります。

　　切片＝6

　　ｙの増加量＝2　　       　2
　―――――――――＝――
　　χの増加量＝3　　     　3

　ｙ＝−2/3χ＋6

　これで、2つの直線の式ができました。

　　　y＝3
　｛
　　　ｙ＝−2/3χ＋6

　　（3）＝−2/3χ＋6

　　　3＝−2/3χ＋6

　　−2/3χ＋6＝3

　　−2/3χ＝3−6

　　−2/3χ＝−3

　　　χ＝−3×−3/2

　　　χ＝9/2

　　　
　　　2つの直線の交点の座標は　χ＝9/2

　　　　　　　　　　　　　　　　　　　　　 y＝3

   答え　χ＝9/2、y＝3  

　（２）

　　　　右上がりの直線から考えます。

　　　　　　　　　　（ｙの増加量）　　　　2
　　　（傾き）は　、――――――＝――＝2
　　　　　　　　　　（χの増加量）　　 　1

　　　右上がりの直線ですから、傾きの符号は（＋）になります。

　　　（切片）は、3

　　　　ｙ＝ａχ＋ｂ

　　　　ｙ＝（傾き）χ＋（切片）

　　　　ｙ＝　２　　χ＋3

　　　次に、右下がりの直線を考えます。

　　　右下がりですから（傾き）の符号は（−）になります。

　　　　　　　　　　（ｙの増加量）       　1
　　　（傾き）は　、――――――＝――＝1/2
　　　　　　　　　　（χの増加量）      　2　　　　

　　　（切片）は、2

　　　　ｙ＝ａχ＋ｂ

　　　　ｙ＝（傾き）χ＋（切片）

　　　　ｙ＝　−1/2　　χ＋　2

　　
　　　　ｙ＝2χ＋3
　　｛
　　　　ｙ＝−1/2χ＋2

　　　　−2χ＋ｙ＝3
　　｛
　　　　1/2χ＋ｙ＝2

　　　　−2χ＋ｙ＝3< BR>　　｛
　　　　2χ＋4ｙ＝8

　　　　−2χ＋ｙ＝3
　　＋）　2χ＋4ｙ＝8
　　　　　　      5ｙ＝11

　ｙ＝11/5

　　　1/2χ＋ｙ＝2　に　ｙ＝11/5　を代入します。

　　1/2χ＋（11/5）＝2

　　1/2χ＝2−11/5

　　1/2χ＝10/5 −11/5　

　　1/2χ＝ −1/5

　　χ＝ −2/5

　　　2つの直線の交点の座標は　χ＝−2/5

　　　　　　　　　　　　　　　             　 y＝11/5

   答え　χ＝−2/5、y＝11/5