中学2年数学 1次関数 3まとめテスト3・解答
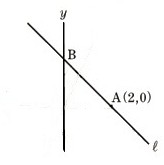
3、図 は、座標軸と y=−χ+b で表される直線ℓをかいた後、χ軸だけを消したものになります。直線ℓは、点A(2,0)を通り、y軸と点Bで交わっています。このとき、次の問いに答えてください。
は、座標軸と y=−χ+b で表される直線ℓをかいた後、χ軸だけを消したものになります。直線ℓは、点A(2,0)を通り、y軸と点Bで交わっています。このとき、次の問いに答えてください。
(1)bの値を求めてください。
y=−χ+bの式に点Aの座標(2,0)を代入します。
0=−2+b
−2+b=0
b=2
答え b=2
(2)図の中に、コンパスと定規を用いてχ軸を作図してください。ただし、作図に用いた線は残してください。
点Aを中心に、y軸に接するように円をかきます。
次に、y軸に接した2点から同じ半径の円を描き、
2つの円の交点と点Aをつなぐ直線を引きます。
できた、直線がχ軸になります。
(3)原点をOとして、直線 y=1/2χ と直線ℓとの交点をCとするとき、次の(ア)~(ウ)に答えてください。
(ア)点Cの座標を求めてください。
点Cの座標は、y=−χ+2 の直線と y=1/2χ の直線の交点になります。
1/2χ=−χ+2
χ=−2χ+4
χ+2χ=4
3χ=4
χ=4/3
y=−χ+2 に χ=4/3 を代入します。
y=−4/3+2
y=−4/3+6/3
y=2/3
交点の点Cの座標がわかりました。
(イ)△OACと△OCBの面積の比を求めてください。
△OACの面積は、(OA)×(C点のy座標)÷2
△OCBの面積は、(OB)×(C点のχ座標)÷2
△OACの面積=2×2/3×1/2
=2/3
△OCBの面積=2×4/3×1/2
=4/3
△OAC:△OCB=2/3:4/3=1:2
答え △OAC:△OCB=1:2
(ウ)△OCBと△OCDの面積が等しくなるような点Dをχ軸上にとります。点Dの座標を求めてください。ただし、点Dのχ座標は負とします。
△OCBは(イ)でわかったので 4/3 になります。
△OCDは(底辺)をODと考えると、(高さ)は、点Cのy座標(2/3)になります。
底辺ODをmとすると、面積は、
m×2/3×1/2=m/3
△OCBと△OCDの面積が等しくなるのですから、
△OCB=△OCD
4/3 = m/3
両辺に3をかければ
m=4 となります。
このmは、辺OD の長さですから、−4 となります。
今回求めているのは点Dの座標で、点Dはχ軸上にありますから
(χ、y)=(−4,0)
答え (χ、y)=(−4,0)















コメント