中学3年数学　二次方程式　確認問題1・解答

中学3年数学　二次方程式　確認問題1・解答

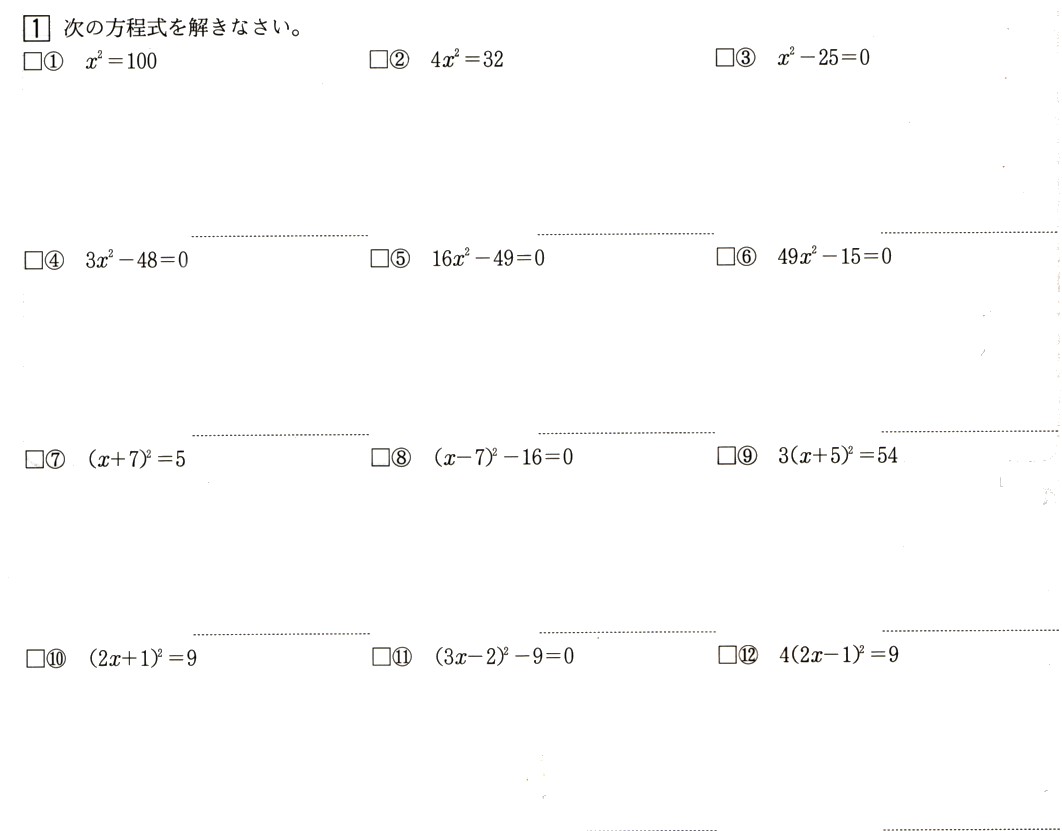
１、次の方程式を解いてください。

?，χ²＝１００

χ＝±√１００

χ＝±√１０×１０

χ＝±１０

答え　±１０

?，4χ²＝３２

４χ²×１／４＝３２／４

χ²＝８

χ＝±√８

χ＝±√２×４

χ＝±２√２

答え　±２√２

?，χ²ー２５＝０

χ²＝２５

χ＝±√２５

χ＝±５

答え　±５

?，３χ²ー４８＝０

３χ²＝４８

３χ²×１／３＝４８×１／３

χ²＝４８／３

χ²＝１６

χ＝±√１６

χ＝±４

答え　±４

?，１６χ²ー４９＝０

１６χ²＝４９

１６χ²×１／１６＝４９×１／１６

χ²＝４９／１６

χ＝±√４９／１６

χ＝±√７²／４²

χ＝±７／４

答え　±７／４

?，４９χ²ー１５＝０

４９χ²＝１５

４９χ ² ×１／４９＝１５×１／４９

χ²＝１５／４９

χ＝± √１５／４９

χ＝±√１５／７

答え　±√１５／７

?，（χ＋７）²＝５

（χ＋７）をＸとします。

（Ｘ）²＝５

Ｘ＝±√５

元の形にします。

(χ＋７)＝±√５

χ＝−７ ±√５

答え　χ＝ー７±√５

?，（χー７）²−１６＝０

（χ−７）²＝１６

（χ−７）をXとします。

（X）²＝１６

X＝±４

元の形にします。

（χー７）＝４
χ＝４＋７
χ＝１１

（χー7）＝ー４
χ＝ー４＋７
χ＝３

答え　χ＝１１、χ＝３

?，３（χ＋５）²＝５４

（χ＋５）をXとします。

３（X）²＝５４

３（X）²×１／３＝５４×１／３

χ²＝１８

χ＝±√１８

χ＝±√２×９

χ＝±３√２

元の形にします。

（χ＋５）＝±３√２

χ＝ー5±３√２

答え　χ＝ー5±３√２

?，（２χ＋１）²＝９

（２χ＋１）²をXとします。

（X）²＝９

X＝±３

（２χ＋１）＝±３

２χ＝３ー１
２χ＝２
χ＝１

（２χ＋１）＝ー３
２χ＝ー３ー１
２χ＝ー４
χ＝ー２

答え　χ＝１、χ＝ー２

?，（３χー２）²−９＝０

（３χー２）²＝９

（３χー２）²をXとします。

（X）²＝９

X＝±３

（３χー２）＝±３

 　　　（３χー２）＝３
３χ＝３＋２
３χ＝５
χ＝５／３

（３χー２）＝ー３
３χ＝ー３＋２
３χ＝ー１
χ＝ー